试题

07年NOIp模拟赛by Matrix67 比赛已顺利结束 题目内容在此发布

/ 30 条评论

2007年10月5日，我举办了一次NOIp模拟赛。现在比赛已经顺利结束了，以下是这次比赛的题目

题目一览

题目名称    Matrix67的情书（二）  送给MM的生日礼物   流言的传播         表白机器人
题目类型    传统                  传统               传统               传统
源文件名称  lovelttr.(pas/c/cpp)  gift.(pas/c/cpp)   rumor.(pas/c/cpp)  robot.(pas/c/cpp)
输入文件名  lovelttr.in           gift.in            rumor.in           robot.in
输出文件名  lovelttr.out          gift.out           rumor.out          robot.out
时间限制    1秒                   1秒                1秒                1秒
内存限制    64M                   64M                64M                64M
测试点      10个                  10个               10个               10个
分值        100分                 100分              100分              100分

Problem 1: lovelttr
Matrix67的情书（二）

问题描述
    28是一个很特别的数字。它是一个完全数，是一个三角形数，是前五个素数的和。天上有28星宿，人有28颗牙齿；土星绕太阳公转一周需要28年，从一只猴子的释放到整座城市的沦陷只需28天。当然，Matrix67偏爱这个数字是有原因的：这是一个关心MM身体和计算安全期都必须用到的数字。总之，Matrix67非常喜欢数字28，他甚至希望数字28能够出现在他给MM写的情书里。
    Matrix67的情书只由数字、大小写字母、空格、换行符和各种英文半角标点符号组成。除去所有其它的字符，仅保留文本中的数字和字母，则整个情书可以看作是一个36进制数。比如，句子“I Love you!”可以转化为1457771337246，因为(ILOVEYOU)36 = (1457771337246)10。Matrix67希望从情书中截取一个或若干个连续的句子，使得它所对应的十进制数能够被28整除。Matrix67希望知道他的情书中有多少个文本片段满足这样的条件。
    我们认为，只有句号、感叹号、问号三种符号才是句子结束的标志（当然整篇文章的结束也标志着最后一句话结束，即使文章最末尾没有任何标点符号）。Matrix67的情书里保证没有不能表示任何数字的“空句子”，即任意两个句子结束标志之间至少会出现一个数字或字母。

输入数据
    输入数据是一篇合法的英文文章，包括英文大小写字母、数字、空格、回车和半角的标点符号。

输出数据
    输出满足要求的文本片段个数。一个满足要求的文本片段是指一个或若干个连续的句子，将它们当作36进制后得到的数可以被28整除。

样例输入

I WILL SHOW YOU

Yes, I am still amazed that I have you. It's still hard to understand how you chose me. How after just one short conversation you knew I was meant for you. But now I know the truth of your conviction. I've never been with someone who suited me so perfectly. You seduced me with your sexy body and strong spirit, and you've kept me with your tender heart. I know you that I can't have you completely and maybe not even for much longer. But I'm still happy. A part of you has become part of me and that is enough.

You'll laugh when I say this, but I dream about you every night. Probably because I can't see you often enough. But when I'm awake I know that you are the furthest thing from a dream. Sometimes I imagine that you are built from solid rock: a moving statue and an indestructible human being. You absolutely contain yourself and then again much more than yourself. Your confidence is consuming and your perspective is huge. You have no place in your life for jealousy or complaints. My friends seem so small in comparison, with their problems always spilling over onto everyone else.

I want you to know how much you've opened my eyes and helped me truly see myself. Until now, my life has been an undecided back-and-forth, and now I know that I've wasted too much time. But now my direction seems clear, and I have confidence in my future. The past doesn't seem to matter anymore. You've made me see possibilities I would never have imagined before.

Yes, I want to please you. But it's through pleasing you that I'll become a better and stronger person. There is nothing I want more than to transform myself through you. You challenge me to grow beyond myself and leave my weaker self behind. I will show you how beautiful I can be, and I will show you how brilliant I can become. This way, I know I'll always have your love.

Forever yours,

Matrix67

样例输出
6

数据规模
    对于30%的输入数据，输入文件大小不超过50KB；
    对于100%的输入数据，输入文件大小不超过1MB。

Problem 2: gift
送给MM的生日礼物

问题描述
    10月11日是MM的生日，Matrix67打算自己DIY一些抱枕送给MM。Matrix67手中有一块矩形花布，花布分成了M x N个小格子，有些格子的花色相同，有些格子的花色不同。为了使最终成品更美观，Matrix67希望用于DIY的布匹都是正方形的，并且满足布匹花色上下对称且左右对称。为此，他希望能计算出这块花布里一共包含有多少个上下对称且左右对称的小正方形。
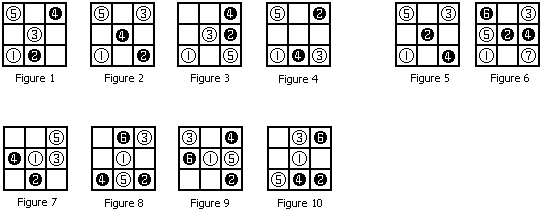
    举例来说，Matrix67手中的花布大小为6 x 4，上面共有5种花色：

ABACDA
DCDEAA
ABABAA
DDCBBA

    则这块布里一共有26个上下对称且左右对称的正方形，其中包括最左上角的3×3正方形、右边4个A组成的2×2正方形，当然还有24个1×1的小正方形。

输入数据
    第一行输入两个用空格隔开的正整数M,N，表示Matrix67手中的格子布分为M行N列。
    以下M行每行N个字符，描述布匹的花色。我们用26个大写字母来区别不同的花色，相同的字母代表相同的花色，不同的字母代表不同的花色。

输出数据
    输出在Matrix67的格子布中切出一块花色左右对称且上下对称的正方形共有多少种方案。

样例输入
4 6
ABACDA
DCDEAA
ABABAA
DDCBBA

样例输出
26

数据规模
    对于30%的数据，M,N<=10；
    对于100%的数据，M,N<=200。

Problem 3: rumor
流言的传播

问题描述
    昨天下午，Matrix67陪MM出去逛街，走累了后去咖啡店歇了歇脚；再后来MM陪Matrix67去了一趟书店，之后两人去电影院看了一场电影。从电影院出来后已经很晚了，考虑到MM的安全问题，Matrix67先送MM回到宿舍，然后自己才回去。第二天Matrix67起床后发现问题严重了：昨天和MM出去玩本来什么都没发生，但现在一些不堪入耳的流言正疯狂传播，很多细节都说得有鼻子有眼的。在澄清事实并抓出元凶的同时，Matrix67希望切断一些流言传播的路径，尽可能减缓流言传播的速度。
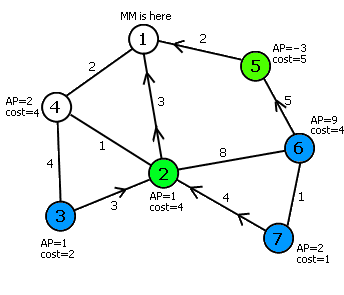
    除去Matrix67和他的MM，学校里还有N个人。这N个人形成了M对双向的朋友关系，这些朋友关系连通了所有N个人。不同的朋友间传递消息的速度各不相同。如果A和B是第i对朋友，那么当其中一个人听到流言后，他会在Ti的时间内传给另一个人。现在，Matrix67只知道流言并没有传遍整个学校，但他不知道哪些人已经听说了这个流言。他希望切断尽可能少的朋友关系，使得无论是哪些人已经获知了流言，流言都无法以原来的速度传给一个新的人（即新的得知此流言的人的出现将变得更晚）。换句话说，Matrix67希望找到一个最小的边集E，使得对任意一个不等于全集的点集S，恰好只有一个顶点在S里的边中权值最小的那一条在边集E中。

输入数据
    第一行输入两个用空格隔开的正整数N和M，分别表示学校的人数和朋友关系数。
    以下M行每行有三个用空格隔开的正整数，其中第i行的三个正整数为Ai, Bi, Ti，表示Ai和Bi是第i对朋友，它们之间传递消息需要Ti的时间。输入数据保证0<Ai≠Bi<=N，0<Ti<=2 000 000 000，且对任意i≠j都有Ti≠Tj。

输出数据
    你需要输出你所得到的最小值和具体的方案。
    输出文件的第一行是一个正整数，代表你的最优方案中需要切断的朋友关系数。
    以下若干行每行一个正整数，表示你的方案里需要切断的朋友关系在输入数据中的编号（即你需要切断的是输入数据中给的第几条边）。这些数必须按照增序排列输出。
    如果有多种最优方案，你只需要输出其中一种即可。我们的评测系统会自动判断你的输出数据的正确性。

样例输入
4 4
1 2 2
4 3 4
2 3 3
1 3 1

样例输出
3
1
2
4

样例说明
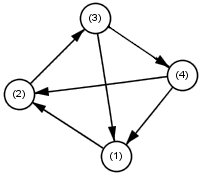
               (1)
                o
               /
            1 /   2
             /    
(4) o——-o——-o (2)
        4  (3)  3  

    首先，(3)—(4)这条边必须去掉，否则若只有4号同学得知流言，流言将以相同的速度传给下一个人。对于其它三条边，只需要去掉权值较小的两条即可，这样不论获知流言的是哪个（些）人，所有可以继续向外传播流言的边中最小的那一条一定已经被去掉了。可以证明，去掉三条边已经是最优的答案了。

数据规模
    对于30%的数据，N<=10，M<=20；
    对于50%的数据，N<=100，M<=1 000；
    对于100%的数据，N<=10 000，M<=100 000。

Problem 4: robot
表白机器人

问题描述
    永远不要以为Matrix67就是传说中的情圣。很少有人知道，Matrix67竟然不好意思主动向MM表白！为此，Matrix67派出他的表白机器人，帮他完成这一项光荣而艰巨的任务。
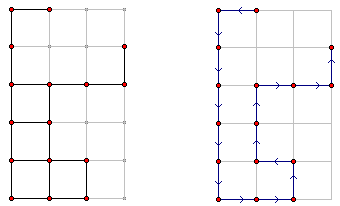
    Matrix67和MM所在的地方可以看作是一个封闭的平面空间，里面分成了M x N个房间，某些房间之间可能有墙。Matrix67总在最左下角的那个房间，MM总在最右上角的那个房间。Matrix67需要给它的机器人输入一系列方向指令，控制机器人避开墙壁到达MM所在的位置。如果L表示向左移一格，R表示向右移一格，U表示向上移一格，D表示向下移一格，那么在下图所示的4×4平面地图里，命令序列RURUUR可以让机器人从起点（左下角）到达终点（右上角）。

#—#—#—#—#
|       |     F |
#   #   #   #—#
|       |       |
#   #   #   #—#
|   |           |
#   #   #   #   #
| S             |
#—#—#—#—#

    但问题远远没有这么简单。由于设计上的缺陷，Matrix67的机器人只能记忆K条指令。这就意味着，当机器人的行走路线过长时，指令不一定能完整地输入机器人。这怎么办呢？Matrix67想到一个好办法：如果让机器人反复执行预先给定的K条指令，那么恰当的指令序列也能使机器人到达终点（虽然这样可能会走很多重复的路）。机器人会忽略所有命令它撞墙的指令。也就是说，如果下一个指令对应的方向上是一面墙的话，机器人将跳过该指令。Matrix67希望知道，是否存在一个长度为K的命令序列，若机器人反复执行这段指令，最终会到达MM所在的地方。对于上面给出的例子，当K=4时，RRLU是一个合法的答案。

输入数据
    第一行输入四个用空格隔开的正整数M、N、W和K，表示该平面区域内有M行N列小房间，房间与房间之间共有W面墙，Matrix67需要给机器人输入的指令长度为K。
    以下W行每行四个数Ai, Aj, Bi, Bj，表示第Ai行Aj列的房间与Bi行Bj列的房间之间有一面墙。

输出数据
    你的输出数据应该是一个由L、R、U、D四种字符组成的长度为K的字符串，表示一个合法的指令序列。机器人反复执行这串指令后最终可以到达右上角的房间。
    输入数据保证有唯一解，因此你不用考虑多解或无解的情况。

样例输入
4 4 5 4
1 2 1 3
2 2 2 3
1 4 2 4
2 4 3 4
3 1 3 2

样例输出
RRLU

数据规模
    对于30%的数据，K<=4；
    对于100%的数

重庆晨报新闻一则：你还会做初三数学题吗

/ 70 条评论

    本想找份假期家教工作，没想到却被家长的一道数学题考倒了。昨日下午，重庆邮电大学大二学生小王显得非常郁闷，而出题面试的家长刘先生却称这是选择家教的有效标准。

先解初三数学题
    小王说，昨日上午经同学介绍，他到家住南坪的刘先生家，应聘当家教。没想到见面后，刘先生拿出了一张写有试题的白纸，说这是读初三的女儿暑假作业上的一道题，做出来了才能当家教。
    题目为：如果a+b+c=0，1/(a+1)+1/(b+2)+1/(c+3)=0，那么(a+1)^2+(b+2)^2+(c+3)^2的值为多少。小王说，当时他做了十多分钟，都没有做出来，感觉有点丢脸，便主动告辞了。
    “不过我还是很不服，回来给几个同学做了，也没有做出来。”小王说，这种题以前读书时也做过，解这种题需要特殊的方法，这么多年没做了当然不记得了。不过这并不代表能力不行，家长用这种方法太武断了。

家长称并非刁难
    随后，记者通过电话联系上了刘先生，他表示这并不是存心刁难，而是有个判断的标准。
    刘先生说，这题目是从女儿假期作业中挑的一道难题，就是想通过试题来测试出应聘大学生的水平。现在假期当家教的大学生很多，但素质却并不一定都好，以前给孩子也请过大学生当家教，效果并不理想，所以现在才想出了这个方法。

不会做的自觉在下面留言
设x=a+1, y=b+2, z=c+3，则x+y+z=6，(x+y+z)^2=36，即x^2 + y^2 + z^2 + 2(xy+yz+xz) =36。
又 1/x + 1/y + 1/z = 0，即xy + yz + xz = 0，因此x^2 + y^2 + z^2 = 36

Matrix67生日邀请赛顺利结束 题目内容在此发布

/ 17 条评论

07年5月12日晚我举办了一次OI生日邀请赛，比赛已经顺利结束。下面是这次比赛的全部试题：

题目一览

题目名称    为什么最少            身高控制计划        狼的复仇          和MM逛花园
题目类型    传统                  传统                传统              传统
源文件名称  whyleast.(pas/c/cpp)  height.(pas/c/cpp)  wolf.(pas/c/cpp)  garden.(pas/c/cpp)
输入文件名  whyleast.in           height.in           wolf.in           garden.in
输出文件名  whyleast.out          height.out          wolf.out          garden.out
时间限制    1秒                   1秒                 1秒               0.1秒
内存限制    64M                   64M                 64M               64M
测试点      10个                  10个                10个              10个
分值        100分                 100分               100分             100分

Problem 1: whyleast
为什么最少

问题描述
    时间过得真快，16号就是我的19岁生日了。为了让自己在新的一岁里人品加加，本菜鸟特地准备了原创菜题大餐供各位大牛享乐，希望大家人人400分。我们今天的第一题巨菜无比，此题乃经典的Hanoi塔问题。在1号塔上有n个盘子，你需要按照Hanoi塔的要求把所有的盘子都移动到3号塔上。
    我一直想不通的是，为什么那些智力题总是要求人们用最少的步骤完成题目中的要求。为什么非要最少呢？这次我们来点特别的，我希望你的程序能够用最多的步数达到要求，而且在此过程中不重复出现任何一种状态。

输入数据
    输入数据只有一个正整数n，表示Hanoi塔问题的金片个数。

输出数据
    第一行输出在不重复出现状态的情况下完成n阶Hanoi塔的最多步数。
    以下若干行依次表示你的操作步骤，每一行两个数a,b表示在这一步应该把a号柱最顶上的金片移动到b号柱上。
    如果有多种方案，你只需要输出其中一种即可。评测系统可以判断你的方案的正确性。

样例输入
2

样例输出
8
1 2
2 3
1 2
3 2
2 1
2 3
1 2
2 3

数据规模
    对于所有数据，n<=12。

附：Hanoi塔问题简介（摘自http://www.matrix67.com/blog/article.asp?id=29）

    法国数学家艾得渥·卢卡斯(Edouard Lucas)于1883年在一份杂志上介绍了一个引人入胜的数学谜题——汉诺塔(Tower of Hanoi)，并称这与古印度的一个传说有关。显然传说的具体内容已经不在本文论述的范围内了，但我想简单的介绍一下。
    相传印度有座大寺庙，它曾被认为是宇宙的中心。神庙中放置了一块上面插有三根长木钉的木板，在其中的一根木钉上，由上至下放了64片直径由小至大的圆环形金属片。古印度教的天神指示他的僧侣们将64片金属片全部移至另一根木钉上。移动规则只有两个：
        1.在每次的移动中，只能移动一片金属片；
        2.过程中任意时刻必须保证金属片小的在上，大的在下。
    直到有那么一天，僧侣们能将64片金属片按规则从指定的木钉上全部移至另一根木钉上，那么，世界末日即随之来到，世间的一切终将被毁灭，万物都将至极乐世界。
    这个传说经常被认为是卢卡斯教授为推广这个数学谜题而捏造的，但不管怎么说，卢卡斯是成功了。这玩意儿变成了家喻户晓的益智游戏之一，后来又成为了学习递归的必修课程。

Problem 2: height
身高控制计划

问题描述
    不要总以为MM只担心自己的体重。经过Matrix67的观察，他发现他身边的MM们更关注自己的身高。MM们都希望自己能长高一些但不要长得太高。如果两个MM的身高相差不多，矮的MM会羡慕较高的MM，希望能长得和她一样修长；如果两个MM的身高相差太大，高的MM反而会想变得和较矮的MM一样娇小。Matrix67为了控制GF们的身高，采取了一项身高控制计划：任意两个女生A和B之间，假设A要比B高一些，如果A高出B的1/4，则A应该以B的身高为目标；相反，如果A的身高小于等于B的1.25倍（但仍然比B高），则B应该努力向A的身高看齐。我们假设不存在身高相等的MM。这样，Matrix67的n个MM之间产生了n(n-1)/2个单向的“榜样”关系。
    之后，Matrix67发现，这样的关系设定存在一个问题：有可能出现A以B为学习目标，B以C为学习目标，C又以A为学习目标的情况。这不相当于自己是自己的榜样么？这样的循环非常可笑，显然是不科学的。Matrix67希望调整一些关系的方向从而消除所有的循环。Matrix67每次改变其中一对MM之间的关系方向，你需要写程序判断，每一次改变后n个MM之间的“榜样”关系是否存在循环。

输入数据
    第一行输入两个用空格隔开的正整数n和m，分别表示MM的个数和改变方向的总次数。
    以下n行每行一个数，其中第i行表示编号为i的MM的身高。为了避免身高相等的情况，高度值已经被“放大”过，所有高度均为不超过2 000 000 000的正整数。
    接下来的m行里每行有用空格隔开的两个不相等的正整数A, B，表示Matrix67对编号为A的MM和编号为B的MM之间的单向关系进行反向。

输出数据
 &nbs
p;  对于Matrix67的每一次操作，你需要输出是否存在某个MM以自己为学习目标的情况（即关系图中是否存在循环）。如果是，则输出“YES”，如果不是，请输出“NO”。
    你的输出应该有m行。

样例输入
4 3
10
7
8
9
3 4
1 2
4 1

样例输出
YES
NO
YES

样例说明
        
    10超过了7的5/4，因此身高为10的MM向身高为7的MM学习；
    10小于等于8的5/4，因此身高为8的MM向身高为10的MM学习。
    同样地，还有9–>10,7–>8,9–>7,8–>9。
    这一组关系中存在多个循环，比如①–>②–>③–>①，再比如①–>②–>③–>④–>①。
    第一次Matrix67将改变③和④之间的方向，这消除了上述第二个循环，但前一个循环仍然存在。
    第二次Matrix67将改变①和②之间的方向，此时关系图中已经不存在循环了。
    第三次Matrix67改变了①和④之间的方向，这将导致新的循环①–>④–>③–>①的出现。

数据规模：
    对于30%的数据，n<=10, m<=100；
    对于50%的数据，n<=100, m<=1000；
    对于70%的数据，n<=1000, m<=100 000；
    对于100%的数据，n<=100 000, m<=100 000。

Problem 3: wolf
狼的复仇

问题描述
    山谷里有n座森林，这些森林从1到n编号。某些森林之间有小路相连，总共m条小路连通了这n座森林，任意两座森林之间都有至少一条路径可以互相到达。
    很久很久以前，这里是狼的家园。在每一座森林里都有一匹狼，每一匹狼都静静地守护着它所在的森林。直到有一天，人类出现了。它们疯狂地开垦1号森林，并且杀死了1号森林的狼。以后，这座森林就好像属于人类了一样，不时有人来到1号森林。其余的n-1匹狼不愿看到悲剧再次发生，它们希望集合它们的力量，为种族，为大自然报仇。
    机会来了。一次偶然的机会，大灰狼们获得了一个重要的情报——有一个小MM经常独自游荡于1号森林。消息传遍了整个狼群，小MM细腻的皮肤和鲜嫩的肉令它们的血液沸腾起来，每一匹狼都幻想着能扑上前去撕裂MM的身体，舔拭那温热的血液。唯一的问题是，它们需要尽快察觉小MM的出现并快速奔向目的地。但由于山谷地形复杂，在第一时间里观察到小MM的出现谈何容易。因此，狼群计划在某些森林建立瞭望塔。当小MM再次出现在1号森林里时，所在的森林里有瞭望塔的狼可以立即发现这一情况，并且沿着最短路径奔向MM。有时最短路不止一条，在途中每当有多条路可以选择时，狼总会选择前往编号较小的森林。这些狼的行动将唤起最短路上沿途经过的狼，这些最短路上的狼将会闻声而起，一同对MM发起进攻。每匹狼都有自己的攻击力，最终对小MM的攻击力即是所有到达1号森林的狼的攻击力总和。注意攻击力的值有可能为负数，因为有一些狼很可能会“拖后腿”，对整个种族的复仇计划反而不利。
    由于森林的地形不同，在不同的地方建造瞭望塔需要的材料不同。现在狼群里一共有k个单位的建筑材料，并且它们已经计算出在n-1座森林中建造瞭望塔各自需要的材料数目。请你来计算一下，在哪些森林里建造瞭望塔可以使得最终到达1号森林的狼群攻击力总和最大。当然，建筑材料不一定要全部用完，但你的方案所需要的建筑材料不能超过总的材料数k。

输入数据
    第一行输入三个用空格隔开的正整数k, n, m，分别表示材料的总数量，森林的数量和小路的数量。1号森林总是MM出没的地方，其余n-1座森林是狼所在的地方。
    第二行到第n行每行有两个用空格隔开的整数，依次表示2号森林到n号森林里的狼的攻击力和在这里建造瞭望塔所需要的材料数。狼的攻击力绝对值不超过10000（可能为负数），每个瞭望塔的材料耗费都是不超过100的正整数。
    接下来m行每行有三个用空格隔开的数x,y,d，表示在x森林和y森林之间存在一条长度为d的路。路的长度是不超过10000的正整数。

输出数据
    输出在满足材料数限制下建造瞭望塔，最多可以给MM带去多大的攻击力。

样例输入
8 7 10
1 4
1 2
2 4
-3 5
9 4
2 1
1 4 2
4 3 4
2 3 3
5 1 2
2 4 1
1 2 3
6 7 1
2 7 4
2 6 8
5 6 5

样例输出
10

样例说明
    输入数据如下图所示，我们用AP来表示攻击力，用cost来表示瞭望塔的材料花费。在涂有蓝色的节点上建造瞭望塔花费仅为7，由于7<=8，因此这种方案未超过材料预算。我们下面计算这种方案所带来的攻击力。
        
    这三匹狼的行走路线已经用箭头表示了出来。注意3号森林和7号森林的狼有多个到达节点1的最短路径，它总是选择标号较小的节点前进。这些路线经过了两个绿色的节点，这两个绿色的节点所对应的狼的攻击力也将加入总攻击力中（必须加入计算且仅算一次）。这种方案的攻击力为1+1+2+9-3=10。事实上，攻击力最大为10，没有其它的建造方案使得总攻击力大于10且材料花费不超过8。

数据规模
    对于30%的数据， k<=1, n<=10, m<=100
    对于50%的数据， k<=10, n<=100, m<=1000
    对于100%的数据，k<=100, n<=1000, m<=10000

Matrix67提醒各位女同学：独自外出时请注意安全。

Problem 4: garden
和MM逛花园

问题描述
    花园设计强调，简单就是美。Matrix67常去的花园有着非常简单的布局：花园的所有景点的位置都是“对齐”了的，这些景点可以看作是平面坐标上的格点。相邻的景点之间有小路相连，这些小路全部平行于坐标轴。景点和小路组成了一个“不完整的网格”。
    一个典型的花园布局如左图所示。花园布局在6行4列的网格上，花园的16个景点的位置用红色标注在了图中。黑色线条表示景点间的小路，其余灰色部分实际并不存在。
        

    Matrix67的生日那天，他要带着他的MM在花园里游玩。Matrix67不会带MM两次经过同一个景点，因此每个景点最多被游览一次。他和他的MM边走边聊，他们是如此的投入以致于他们从不会“主动地拐弯”。也就是说，除非前方已没有景点或是前方的景点已经访问过，否则他们会一直往前走下去。当前方景点不存在或已游览过时，Matrix67会带MM另选一个方向继续前进。由于景点个数有限，访问过的景点将越来越多，迟早会出现不能再走的情况（即四个方向上的相

非传统题型练习：解析一道循环赛题目

/ 5 条评论

Problem: game 取数游戏
题目来源：Matrix67根据经典问题改编

问题描述
    选数游戏是一个两人游戏。两人将轮流从1到9这九个数字中取数，取过的数不能再取。我们规定，谁取到的数里能找到三个数，使得这三个数的和为15，谁就获得了这次游戏的胜利。如果A取了1、6、7三个数，B取了2、3、5，若这时该A继续取数，则A取8可以获得胜利，因为当A获得了数字8后，出现了1+6+8=15。
    在游戏的每一着中，你可以得到此时游戏的状态。请你编程选择一种赢得游戏的最佳策略。

输入格式
    第一行输入若干个用空格隔开的数，表示你已经取了的数。这些数递增排列。
    第二行输入若干个用空格隔开的数，表示对手已经取了的数。这些数递增排列。
    当某一行没有数字（某个游戏者还没有选数）时，该行仍然会留出位置。

输出格式
    输出你认为此时你的最佳选择。

样例输入
1 6 7
2 3 5

样例代码
    下面的代码演示了游戏的这样一个策略：每一次总是选择最大的没有被取过的数。

program game;
var
   hash:array[1..9]of boolean;
   i:integer;
begin
   assign(input,'game.in');
   reset(input);
   repeat
      read(i);
      hash[i]:=true;
   until eof;
   close(input);

   for i:=9 downto 1 do
      if not hash[i] then break;
   assign(output,'game.out');
   rewrite(output);
   writeln(i);
   close(output);
end.

评分方法
    该题目将通过选手之间的循环赛进行评分。
    在某两个选手对抗时，测试程序将导入这两个选手的源程序并进行编译，然后轮流为选手编写输入文件实时描述对战情况。选手的输出文件将作为此次选手的决策提交上来。当游戏已经出现获胜方或无法继续进行时，测试程序自动结束。每两个选手比赛时将分两场进行，一场对抗后先行者将进行交换。任一次对抗中，选手胜一场得2分，负一场得-2分，平一场得0分（这个分数不是选手该题的最后得分）。对比赛得分进行排名后，若总选手数为n，你的排名为i，那么你的得分为(n-i+1)*100/n。得分为小数则取下整。排名相同则平分该段得分。
    选手程序出现以下情况将作为该次对抗的负者处理：
        选手程序单着运行时间超过1秒；
        选手内存占用超过64M；
        选手程序未输出决策或输出错误；
        选手程序非正常退出；
        选手程序发生错误导致评测程序非法退出。

    大家有没有看出来，这个游戏就是一个井字棋游戏。3个数加起来等于15一共有8种情况，而这8种情况恰好对应一个3阶幻方中的三个横行、三个纵列和两个对角线。也就是说，如果把这个游戏想成在下面的棋盘中进行，那就和井字棋游戏没什么两样了。

   +—+—+—+
   | 8 | 1 | 6 |
   +—+—+—+
   | 3 | 5 | 7 |
   +—+—+—+
   | 4 | 9 | 2 |
   +—+—+—+

    关于井字棋游戏，之前我曾有过研究。
    原来学博弈论之类的东西时，我曾写过一个程序，计算井字棋游戏的最佳策略。但不管我怎么搞，这个程序总是先走最角落的位置，这是十分可笑的。我一直在想，我的程序哪点儿有问题。后来我想到了。我的程序没有任何问题，而是人的习惯性思考出的错。我的程序计算出来的结果是对的，在井字棋游戏中开局占领一个角的胜算最大。

    比如说，现在我占了最左下角的那一个位置。那么下一步如果你走的是画了“X”的位置，你就输了。

   +—+—+—+
   | X | X | X |
   +—+—+—+
   | X |   | X |
   +—+—+—+
   | O | X | X |
   +—+—+—+

    下面的图1到图4这四个棋谱，它包含了除第二步走中间以外所有的分支情况。可以看出，如果你第二步不占领中间的话，你是必败的。
    图5告诉我们，即使对手占住了中间，第四步棋也有2/6个陷阱可以置他于死地。而另外4/6将导致棋局最终打平。假设每一步对方都是随机走的话，打到图6的情况概率为(1/8) * (4/6)，约为8.33%。反过来，我的胜算超过了90%。这在理论上可能是最大的了。
    当然，对手没有那么傻。面对这种情况，理智的人第二步总会想要占领中间的格子。考虑到这一点的话，胜算或许不到50%。

    仔细思考，你会发现，如果你第一步占领了中间的话，胜算是可以达到50%的。图7表明了这样一种情况，如果你第一步走中间，而对手不小心走到了边上，那么他就完了。比起前面的那些来，这里的陷阱可能更隐蔽一些。
    剩下的三个图表明，对手走了4个角中的一个后，最终结果必然是平局。

    至于以上这么多棋谱到底该选用哪一个，这个决策是属于自己的。

    我们考虑自己先行的所有情况的同时，也看清了自己作为后行者可能遇到的陷阱。对照以上棋谱，我们可以轻易获得平局的结果。

    由于井字棋游戏的总的情况数也只有那么多，变数不大，因此这个东西是一个非常入门级的东西。实际写程序的时候，分类讨论的效果比博弈树更好。

Matrix67原创
转贴请注明出处

非传统题型练习：三道交互式题目

/ 3 条评论

Problem 1: famous 谁是名人
题目来源：Matrix67根据经典问题改编

    题目和测试库源码直接见http://www.matrix67.com/blog/article.asp?id=179

题解：
    显然名人最多有一个。问两个还没有问过的人A和B。如果A认识B，那么A肯定不是名人；如果A不认识B，那么B肯定不是名人。总之，结果无论是什么，总有一个人要排除。由于题目说了一定有名人，那么只需要询问n-1次，每次排除一个人，剩下的肯定就是名人了。

Problem 2: meandian 中等工资
题目来源：CEOI 2006 有细节改动 (Translated by Matrix67)

问题描述
    一些公司不愿意透露员工的工资，这样可以防止工会的领导者知道员工的报酬有多低，从而避免烦人的涨工资的谈判。不过，有时公司很乐意为统计和市场目的透露一些消息。
    其中一个公司愿意回答的问题是这样的形式：“员工A、B、C、D的中等工资是多少”。四个数的“中等值”定义为中间的两个值的算术平均数。更明确的，a,b,c,d的中等值按这样的方式得到：首先对这四个数排序，然后计算排序后的第二个数x和第三个数y的平均数(x+y)/2。你的目标是通过询问一些这种形式的问题来得到员工具体的工资数。注意有一些员工的工资有可能永远不能推出（比如工资最低的那个人）即使所有可能的问题都被问过。
    该公司有N(4<=N<=100)名员工，分别用1到N标记。每个员工的工资是一个小于等于100 000的正偶数，且没有两个员工的工资相同。
    你将得到一个实现中等值的询问的库。给出四个不同的整数A,B,C,D (1<=A,B,C,D<=N)，这个函数可以返回员工A、B、C、D的中等工资。
    写一个程序访问测试库，找出所有员工准确的工资数（除了永远不能确定的以外）。你的程序最多允许询问1000次问题。

交互方法
    你将获得的测试库提供了以下三个函数或过程：
       function init:longint;
       function meandian(a,b,c,d:longint):longint;
       procedure solution(var sol:array of longint);
    Init：调用该函数不带参数。这个函数必须在程序开头调用且只能调用一次。它将返回一个整数N，即公司的员工数。
    Meandian：这个函数被调用时需要带四个参数A、B、C、D。这四个数应该是从1到N的四个不同的数（包括1和N）。它返回一个整数，是员工A、B、C、D的中等工资。
    Solution：这个函数应该在程序结尾调用。你需要用一个表示员工工资的整数数组来作为它的参数。如果某个员工的工资不能确定，数组中对应的值应该为-1。
    注意这个数组必须从0开始。也就是说员工1的工资应该在数组的0位置，员工2应该在1的位置，依此类推。

    你的源程序在声明处必须包含“uses libmean”。
    编译时，你需要把库文件和源文件放在同一个目录。

一个成功交互的例子
    下面是一个程序代码的片段。它完全不能解决我们的问题，但它可以告诉你如何使用库函数。

uses libmean;
var i, n : integer;
    arr : array[0..99] of longint;
    foo, bar, quux : integer;
begin
   n := Init;
   foo := Meandian(1, 2, 3, 4);
   bar := Meandian(4, 2, 3, 1);
   quux := Meandian(n, n-1, n-2, n-3);
   for i := 1 to n do
      arr[i-1] := 2*i;
   arr[3] := -1;
   Solution(arr);
end.

你如何测试自己的程序
    我们提供的库允许你通过标准输入读进数字N和N个偶数来测试你的程序。
    这个库将输出一个信息告诉你你的答案是否正确。它同时产生一个包含有你的程序运行的详细信息的文本文件meandian.log。
    下面的例子告诉你如何为你的程序输入数据。测试库将告诉你你的答案的正确性。
10
100 500 200 400 250 300 350 600 550 410

评分方法
    当你提交的答案与我们的正确答案相符时得10分。我们一共将有10次测试，总共100分。
    出现以下情况均不给分：
      程序提交的答案错误或没有提交答案；
      程序运行时间超过0.1秒；
      程序使用内存空间超过64M；
      程序询问次数超过1000次；
      程序崩溃或意外退出；
      错误访问库导致测试库出错；
      程序访问了其它外部文件。

数据规模
    对于30%的数据，N<=10；
    对于50%的数据，N<=50；
    对于100%的数据，N<=100。

题解：
    当时我做同步赛时，只有这道题AC了，因此对这道题情有独钟。
    如果N=4，那么显然一个都问不出来。那么N=5呢？通过下面的方法可以问出这5个人中工资排在中间的那个人是谁，并且知道他的具体工资数。假如这5个人按工资从低到高排序分别为A、B、C、D、E，那么问ABCD和ABCE将得到两个相等的小值（BC的平均数），问ACDE和BCDE将得到两个相等的大值（CD的平均数）。剩下的结果由ABDE产生，其值介于前面两者之间（BD的平均数）。换句话说，把5种问法问个遍，那么得数最大的就是CD的平均数，得数最小的是BC的平均数，剩下的那个就是BD的平均数。根据这三个式子，我们就可以算出BCD的值是什么了。但我们只知道了三个人的工资数，还不知道哪个人对应哪个人。你会发现，你不能确定B和D具体是哪个人，但C是谁我们肯定知道。C所对应的人就是问出BD的平均数的那一次询问里没有被问到的人。
    询问5个人可以问出一个人来，那么我们就不断地找5个都还不知道的人重复这个过程。我们不必真的去“找”工资还没确定的人，只需要用一个新的人来代替前一个5人组中问出来了的那个人。这样下去我们只需要不到500次就可以问出N-4个人的具体工资。这种方法不能确定工资最小的两个人和工资最大的两个人。
    事实上，我们可以证明这4个人永远不可能被问出来。假如把工资最小的两个人它们对应的工资数交换一下，你会发现所有可能问到的问题答案仍然不变，因此这两个人不能判断谁是谁。对于工资最大的两个人道理相同。

Problem 3: gf 谁是我的女友
题目来源：Matrix67根据经典问题改编

问题描述
    我们学校有M个男生，N个女生（M<=N<=1000）。每个男生都在这些女生中找到了一个知己。每个男生都恰有一个女友，不同的男生有不同的女友（有N-M