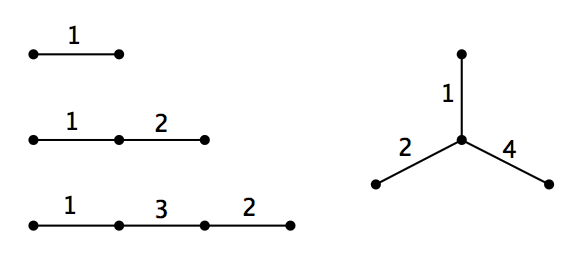
还记得小时候有一道经典奥数题,大概是让你把两个数字 1 、两个数字 2 、两个数字 3 和两个数字 4 排成一个 8 位数,使得其中两个数字 1 之间正好夹着 1 个数字,两个数字 2 之间正好夹着 2 个数字,两个数字 3 之间正好夹着 3 个数字,两个数字 4 之间正好夹着 4 个数字。稍作尝试便可得出正确答案: 4, 1, 3, 1, 2, 4, 3, 2 。如果把逆序后的数列视作本质相同的数列,那么上面这个答案是唯一的。这个问题是由 C. Dudley Langford 在 1958 年提出的,因此我们把它叫做 Langford 数列。
当 n = 3 时, Langford 数列也是唯一的: 2, 3, 1, 2, 1, 3 。我小时候曾经没日没夜地试图寻找 n = 5 时的 Langford 数列,结果却怎么也找不到。后来才知道, n = 5 时的 Langford 数列根本就不存在。这是为什么?你能证明这一点吗?