n 个小朋友在圆桌上坐成一圈。初始时，每个小朋友都拥有一定数量的糖。接下来，反复进行下面两个操作：
1. 如果有人手里的糖数是奇数，就向老师再要一颗糖，把手里的糖数补成偶数；
2. 每个人都把自己手中一半的糖传给他右边的人（同时接到从左边传过来的糖）。
证明：总有一个时刻，所有小朋友手中都会拥有相同数量的糖。
附加题：这是一个非常经典的问题。猜猜看我最早在什么地方看到的这个问题？
证明
经典证明：能否在平面上写下不可数个不相交的Y？
这篇文章收录了 Which Way Did the Bicycle Go 趣题集中一个非常有趣的问题：是否有可能在平面上画不可数个不相交的 8 ？答案是否定的。证明方法非常简单。对于任意一个 8 字形，在两个洞里各取一个有理点 P 、 Q （由于平面上的有理点是稠密的，这是总能办到的），则称这个 8 字形圈住了有理点对 (P, Q) 。注意到由于 8 字形不能相交，因此两个 8 字形不可能圈住同一对有理点。由于平面上的有理点对是可数的，因此 8 字形的数量也是可数的。
注意到，平面上显然能够容下不可数个不相交的直线段，也显然能够容下不可数个不相交的圆（比方说一系列同心圆）。在 Mathematical Puzzles 一书里， Peter Winkler 提出了这样一个问题：我们能在平面上写下不可数个不相交的字母 Y 吗？
如果对Heron公式求导的话
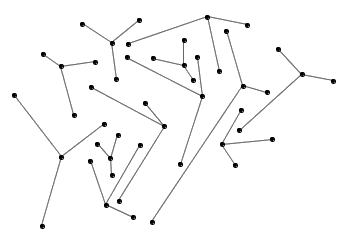
Heron 公式是一个已知三角形三边长便能直接求出其面积的经典公式。把三角形的三边长分别记作 a 、 b 、 c ，令三角形的半周长 p = (a + b + c) / 2 ，则三角形的面积可以用 Heron 公式 S = √p(p – a)(p – b)(p – c) 求出。如果把 p = (a + b + c) / 2 代入式子，得到的公式其实也挺对称的： S = √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) / 4 。
现在，我们把这个公式看作是一个关于 c 的函数： f(c) = √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) / 4 。它的导数是多少？
注意到，利用平方差公式，根号内的式子可以进一步整理为 ((a + b)2 – c2)(c2 – (a – b)2) ，它的导数是 – 2c(c2 – (a – b)2) + 2c((a + b)2 – c2) = 4c(a2 + b2 – c2) 。因而，整个原函数的导数就是 c(a2 + b2 – c2) / (2 · √(a + b + c)(a + b – c)(a – b + c)(- a + b + c) ) 。
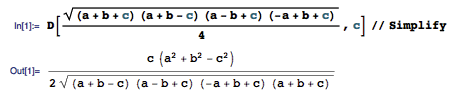
有趣的是，当 a 、 b 、 c 满足勾股定理的关系 a2 + b2 = c2 时，导数值正好为 0 。这是为什么？ Heron 公式的导数的零点和勾股定理有什么联系呢？
UyHiP趣题：按照盒子的三边长之和来计费有没有漏洞？
今天的趣题来自 UyHiP 今年十月的趣题。
许多快递公司都依据物件的长、宽、高三边之和来收费，一些航空公司也要求托运行李的三边长相加不能超过某个限制。那么是否有人想过，有没有可能把一个三边之和较大的盒子装进一个三边之和较小的盒子里，从而骗取更低的费用呢？有人会说，恐怕不行吧，长宽高之和更大的盒子体积不也应该更大一些吗？不见得。比方说，盒子 A 的长宽高分别是 10 、 10 、 10 ，盒子 B 的长宽高分别是 9 、 9 、 12.1 。盒子 B 的三边长之和显然比盒子 A 要大，但体积只有 980.1 ，比前者要小近 20 个单位。那么，为什么就不能把盒子 B 沿斜线方向塞进盒子 A 呢？有人会敏锐地发现，在上面的例子中，盒子 A 的体对角线长为 17.3205 ，但盒子B的对角线长度达到 17.5616 ，显然无法完全放进盒子 A 里。不过且慢，我也能举出这样的例子，三边和更大的盒子其体积和对角线都比小的盒子的要小。盒子 A 的长宽高分别为 10 、 10 、 20 ，盒子 B 的长宽高分别为 7.1 、 16.5 、 16.5 。盒子 B 的长宽高之和比盒子 A 大，体积为 1932.98 ，对角线长度比前者小大约 0.1 。看来，为了解决这个问题，我们还需要从一些更巧妙的方面入手。
趣题：旋转桌子避免灯泡全亮
网友 @ipondering 分享了一个非常精彩的数学趣题集，里面有很多我之前从没见过的趣题，其中有些问题的题目和解答都相当漂亮。近段时间里，我打算从中选一些最精彩的题目来讲讲。今天的题目是该趣题集中的第二题，原题背景涉及到 King Arthur 和 Merlin 的故事，我就舍去简化了。
某个国王手下有 n 个大臣。国王定期主持国家会议，届时 n 个大臣将会间隔均匀地坐在圆桌上。每个座位前都有一盏照明灯，只有所有的灯都亮了，会议才能开始进行。如果有些灯没亮，国王会下达指令，让指定位置上的大臣按下座位前的灯的开关，把没亮的灯都打开。例如，当 n = 100 时，圆桌上会坐着 100 个大臣。不妨将座位从 1 到 n 顺序编号，假设其中编号为 3 、 28 、 97 的座位前没有亮灯。于是，国王下令这三个位置上的大臣按下各自面前的开关，把这三盏灯打开，这样才能开始会议议程。
在这 n 个大臣中，有一个奸臣。这次会议的议题恰好就是商讨对这个奸臣的惩治办法。奸臣知道自己难逃一劫，但他希望能够无限制地拖延会议。他可以在所有大臣就座前精心设置各个照明灯的初始状态，并在国王每次下达指令之后（但在大臣执行命令之前）把圆桌旋转到一个合适的位置，让大臣们按下错误的开关。
对于哪些 n ，奸臣可以始终保证灯不会全亮，从而无限制地拖延会议？对于哪些 n ，国王可以根据局势巧妙地构造指令，使得有限轮指令之后所有灯必然全亮？
在会议结束前，奸臣仍然是 n 个大臣中的一员。国王每次只能下达形如“座位编号为 a1, a2, a3, … 的大臣改变各自面前的灯的状态”的指令。奸臣可以任意旋转圆桌，改变灯与大臣的对应关系。当然，他也可以选择不旋转圆桌。即使桌子被旋转过，所有大臣也必须严格遵守国王的指令。