一个无理数的无理数次方是否有可能是一个有理数？这是一个非常经典的老问题了。答案是肯定的，证明方法非常巧妙：考虑根号 2 的根号 2 次方。如果这个数是有理数，问题就已经解决了。如果这个数是无理数，那么就有：
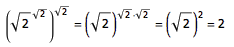
我们同样会得到一个无理数的无理数次方是有理数的例子。
这是一个典型的非构造性证明的例子：我们证明了无理数的无理数次方有可能等于有理数，但却并没有给出一个确凿的例子。毕竟我们也不知道，真实情况究竟是上述推理中的哪一种。那么，真实情况究竟是上述推理中的哪一种呢？ Gelfond-Schneider 定理告诉我们，假设 α 和 β 都是代数数，如果 α 不等于 0 和 1 ，并且 β 不是有理数，那么 α 的 β 次方一定是超越数。根据这一定理我们可以立即看出，根号 2 的根号 2 次方真的是一个无理数，实际情况应该是上述推理中的后者。
那么，是否存在一个无理数 a ，使得 a 的 a 次方是有理数呢？最近， Stan Dolan 证明了这样一个结论：事实上，几乎所有 (1, ∞) 里的有理数都是某个无理数 a 的 a 次方。
Using your Head is Permitted 数学谜题站的主持人 Michael Brand 某日收到了来自 R. Nandakumar 的一个谜题：是否有可能把一个矩形剖分成若干个小矩形，使得每个小矩形的形状互不相同，但它们的面积都一样？没有想到，从这个问题出发，加上一些非常机智巧妙的分析与构造，我们能得到越来越多有意思的东西。于是，它就变成了 Using your Head is Permitted 今年 3 月的谜题。看了谜题的答案后，我也被彻底折服，决定把这一系列的思考重述在此，和大家一同分享。为了简便起见，下面的“矩形剖分方案”一律指的是把一个大矩形分割成若干个小矩形的方案。
想像一个圆盘在地面上滚动一周，那么圆周上一点所形成的轨迹就叫做旋轮线（或者摆线）。旋轮线下方的面积是多少，这是一个非常有趣的问题。据说， Galileo 曾经用一种非常流氓的方法，推测出了旋轮线下方的面积。他在金属板上切出一块圆片，再在金属板边缘剪下这个圆形所对应的旋轮线，把它们拿到秤上一称，发现后者的重量正好是前者的三倍。于是，他推测，半径为 r 的滚轮所产生的旋轮线，其下方的面积就是 3πr2 。
不过，今天我第一次知道，这个结论对于正多边形是同样成立的。
今天看到这里给出了一个“星际争霸是 NP-hard 问题”的一个证明。具体地说，给定一个初始布局（包括地图、双方已有资源、双方已有建筑、双方已有兵力），判断其中一方是否能获胜，这个问题是 NP-hard 的。当然，考虑到即时战略游戏的复杂性，这个结论并不出人意料；真正有趣的，则是如何巧妙地利用游戏中的元素，构造出极其精巧的初始局面，从而转化成某个已知的 NP-complete 问题。下面是原文中给出的证明。这个证明有没有什么漏洞？你还能想到哪些别的证明方法？欢迎在下面留言一同分享。
数列 1, 1, 2, 3, 5, 8, 13, 21, 34, … 叫做 Fibonacci 数列。这个数列有很多神奇的性质，其中一个性质是，每一个 Fibonacci 数的平方与它前后两个 Fibonacci 数的乘积一定正好相差 1 。具体地说，如果把第 n 个 Fibonacci 数记做 Fn ，那么有：
Fn+1 · Fn+1 – Fn · Fn+2 = (-1)n
今天看到了这个定理的一个组合数学证明，觉得非常有意思，在这里和大家分享。