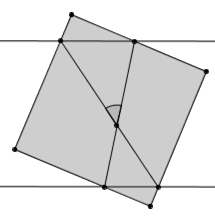
如图，把边长为 d 的正方形放在两条距离也为 d 的平行线之间，于是产生了四个交点。求证，把这四个点交叉相连产生的夹角为 45° 。
证明
经典证明：任意三角形都能被分成n≥4个等腰三角形
证明：对于任意一个三角形和任意一个大于等于 4 的正整数 n ，都存在一种把这个三角形分割成 n 个等腰三角形的方案。这个问题曾经出现在 1976 年的 Crux Mathematicorum 上。 1977 年， Gali Salvatore 给出了一个非常漂亮的解答。
网络流和棒球赛淘汰问题
1996 年 9 月 10 日，《旧金山纪事报》的体育版上登载了《巨人队正式告别 NL 西区比赛》一文，宣布了旧金山巨人队输掉比赛的消息。当时，圣地亚哥教士队凭借 80 场胜利暂列西区比赛第一，旧金山巨人队只赢得了 59 场比赛，要想追上圣地亚哥教士队，至少还得再赢 21 场比赛才行。然而，根据赛程安排，巨人队只剩下 20 场比赛没打了，因而彻底与冠军无缘。
有趣的是，报社可能没有发现，其实在两天以前，也就是 1996 年 9 月 8 日，巨人队就已经没有夺冠的可能了。那一天，圣地亚哥教士队还只有 78 场胜利，与洛杉矶道奇队暂时并列第一。此时的巨人队仍然是 59 场胜利，但还有 22 场比赛没打。因而，表面上看起来，巨人队似乎仍有夺冠的可能。然而，根据赛程安排，圣地亚哥教士队和洛杉矶道奇队互相之间还有 7 场比赛要打，其中必有一方会获得至少 4 场胜利，从而拿到 82 胜的总分；即使巨人队剩下的 22 场比赛全胜，也只能得到 81 胜。由此可见，巨人队再怎么努力，也不能获得冠军了。
在美国职业棒球的例行赛中，每个球队都要打 162 场比赛（对手包括但不限于同一分区里的其他队伍，和同一队伍也往往会有多次交手），所胜场数最多者为该分区的冠军；如果有并列第一的情况，则用加赛决出冠军。在比赛过程中，如果我们发现，某支球队无论如何都已经不可能以第一名或者并列第一名的成绩结束比赛，那么这支球队就提前被淘汰了（虽然它还要继续打下去）。从上面的例子中可以看出，发现并且证明一个球队已经告败，有时并不是一件容易的事。为了说明这一点，我们展示一组虚构的数据（这是在 1996 年 8 月 30 日美国联盟东区比赛结果的基础上略作修改得来的），如下表所示。
| Team | 胜 | 负 | 余 | 纽约 | 巴尔的摩 | 波士顿 | 多伦多 | 底特律 |
| 纽约 | 75 | 59 | 28 | 0 | 3 | 8 | 7 | 3 |
| 巴尔的摩 | 72 | 62 | 28 | 3 | 0 | 2 | 7 | 4 |
| 波士顿 | 69 | 66 | 27 | 8 | 2 | 0 | 0 | 0 |
| 多伦多 | 60 | 75 | 27 | 7 | 7 | 0 | 0 | 0 |
| 底特律 | 49 | 86 | 27 | 3 | 4 | 0 | 0 | 0 |
其中，纽约扬基队暂时排名第一，总共胜 75 场，负 59 场，剩余 28 场比赛没打，其中和巴尔的摩还有 3 场比赛，和波士顿还有 8 场比赛，和多伦多还有 7 场比赛，和底特律还有 3 场比赛（还有 7 场与不在此分区的其他队伍的比赛）。底特律暂时只有 49 场比赛获胜，剩余 27 场比赛没打。如果剩余的 27 场比赛全都获胜的话，是有希望超过纽约扬基队的；即使只有其中 26 场比赛获胜，也有希望与纽约扬基队战平，并在加赛中取胜。然而，根据表里的信息已经足以判断，其实底特律已经没有希望夺冠了，大家不妨自己来推导一下。
趣题：一个与含60度的三角形有关的性质
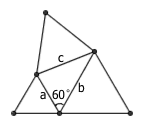
有一个三角形，三边长分别为 a 、 b 、 c ，其中 a 、 b 两条边夹角为 60° 。分别以 a 、 b 、 c 为边向外作等边三角形。求证：前两个等边三角形的面积之和，减去第三个等边三角形的面积，将等于原三角形的面积。
趣题：证明边权递增的路径始终存在
一个树林里有 100 个村庄，它们之间有 1000 条小路，每条小路都连接着两个不同的村庄。每条小路 e 都有一条难度系数 l(e) ，所有小路的难度系数都不相同。现在有一个探险家，他想要选择一条长度为 20 的路径，使得所经过的小路的难度系数不断增加。求证：他总能找到这样的路径。
探险家可以任意选择路径的起点和终点。