组合数学

计算阶乘的另一些有趣的算法

/ 15 条评论

    一个正整数n的阶乘就是前n个正整数的乘积，我们通常需要n-1次乘法操作来算出精确的值。不像等差数列求和、a的n次幂之类的东西，目前求阶乘还没有什么巨牛无比的高效算法，我们所能做的仅仅是做一些小的优化。

更少的乘法运算次数？
    在高精度运算中，乘法计算的速度远远慢于加减法，因此我们有必要减少乘法运算的次数。下面我将做一个非常简单的变换，使得计算阶乘只需要n/2次乘法。继续看下去之前，你能自己想到这个算法来吗？

    我们可以把一个数的阶乘转换为若干个平方差的积。例如，假如我想求9!，我可以把前9个正整数的乘积写成这个样子：
   1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9
= (5-4) * (5-3) * (5-2) * (5-1) * 5 * (5+1) * (5+2) * (5+3) * (5+4)
= (5-1) * (5+1) * (5-2) * (5+2) * (5-3) * (5+3) * (5-4) * (5+4) * 5
= (5^2 – 1^2) * (5^2 – 2^2) * (5^2 – 3^2) * (5^2 – 4^2) * 5
    注意到一个有趣的事实：上面的四个平方差算出来分别是24, 21, 16, 9，它们之间的差正好是连续的奇数（因为n^2等于前n个正奇数的和）。因此，我们可以用初始数(n/2)^2不断减去一个个的正奇数，求出所有n/2个平方差，再用n/2次乘法把它们乘起来。这种算法实现起来非常简单，并且（当n不大时）同样只需要单精度乘高精度，但需要的乘法次数大大减少了。假设我们已经有了一个高精度类，求n!只需要下面几句话：
long h=n/2, q=h*h;
long r = (n&1)==1 ? 2*q*n : 2*q;
f = LargeInteger.create(r);
for(int d=1; d<n-2; d+=2)
   f = f.multiply(q-=d);

更少的总运算次数？
    尽量提取阶乘中的因子2，我们可以得到另一种阶乘运算的优化方法。这很可能是不需要分解质因数的阶乘算法中最快的一种。
    假如我们需要计算20!，我们可以把20拆成若干组正奇数的乘积：

  1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 11 * 12 * 13 * 14 * 15 * 16 * 17 * 18 * 19 * 20
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 2 * 4 * 6 * 8 * 10 * 12 * 14 * 16 * 18 * 20
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 2^10
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 2 * 4 * 6 * 8 * 10 * 2^10
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 2 * 3 * 4 * 5 * 2^15
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 2 * 4 * 2^15
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 1 * 2 * 2^17
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 1 * 2^18

    只需要一次累乘就可以求到每一组奇数的乘积，最后再花费log(n)次乘法把它们全部乘起来。最后的那个2^18也可以二分计算出来。真正的代码还有很多细节上的优化，另外还借用了递归使得操作变得更加简便。你可以在本文最后附的那个链接里去找Split-Recursive算法。

还能再快一点么？
    继续扩展上面的算法，我们可以想到，如果把每个数的质因数都分解出来，并且统计每种质因子有多少个，我们就可以多次使用二分求幂，再把它们的结果乘起来。注意这里并不是真的要老老实实地去分解每个数的质因子。对于每个质数x，我们可以很快算出前n个正整数一共包含有多少个质因子x（记得如何求n!末尾有多少个0么）。这种算法的效率相当高，已经能够满足大多数人的需要了。

另一种诡异的阶乘算法：
    这个算法可能是所有有名字的阶乘算法中最慢的一个了（Additive Moessner算法），它对一个数列进行重复的累加操作，一次次地计算前缀和，总共将花费O(n^3)次加法操作。但是，令人费解的是，这个简单的程序为什么可以输出前n个正整数的阶乘呢？
a[0]:=1;
for i:=1 to n do
begin
   a[i]:=0;
   for j:=n downto 1 do
   begin
      for k:=1 to j do
         a[k]:=a[k]+a[k-1]
      write(a[i],' ');
   end;
end;
    我在网上搜索相关的东西时找到了另一个有趣的东西。对一个初始时全为1的数列反复进行这两个操作：累加求前缀和，然后以1,2,3,…的间隔划掉其中一部分数（即划去所有位置编号为三角形数的数）形成新的序列。类似的数列操作方法最先由Alfred Moessner提出的，我们这里不妨把它叫做Moessner数列。你会发现，第n轮操作开始前，数列的第一个数恰好是n! 。看看下面的例子吧：

1 1 1 1 1 1 1 1 1  1  1  1  1  1  1 …
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 …
x 2 x 4 5 x 7 8 9  x 11 12 13 14  x …

2 4  5  7  8  9 11 12 13 14 …
2 6 11 18 26 35 46 58 71 85 …
x 6  x 18 26  x 46 58 71  x …

6 18 26 46  58  71 …
6 24 50 96 154 225 …
x 24  x 96 154   x …

24  96 154 …
24 120 274 …
x 120  x  …

120 …
…..

    当然，发现前面O(n^3)的程序和这个Moessner数列的关联时我很是吃了一惊：在前面的程序里，如果你输出每一次i循环末所得到的数列，你会发现输出的这些数正好就是后面这个问题里被我们划掉的数，而它们其实就是第一类Stirling数！
    这到底是为什么呢？是什么东西把阶乘、第一类Stirling数、Moessner数列和那个O(n^3)的程序联系在一起的呢？昨天，我想这个问题想了一天，最后终于想通了。如果把Moessner数列排列成这个样子，一切就恍然大悟了：

  
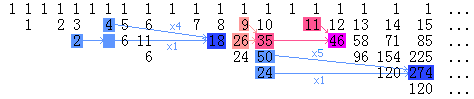
    仔细观察上图，我们会发现：
    1. 按照Moessner数列的定义，每个数都应该等于它左边的数和左上角的数的和（这个“左边”可以跳过若干空格）。例如，35 = 9 + 26，46 = 11 + 35。排成一系列三角形后，每个三角形最右边一列的数就是被划去的数，它永远不能参与它下面的那些行的运算。
    2. 设a[n,i,j]表示左起第n个三角形阵列中的第i行右起第j列上的数，则a[n,i,j]=a[n-1,i-1,j]*n + a[n-1,i,j]，例如274=50*5+24。如果递推时遇到空白位置而它左边隔若干空格的地方还有数的话，则需要用左边的数来补，例如18=4*4+2。对于每个三角形的最后一列来说，这个性质实际上就是第一类Stirling数的递推关系，因此Moessner数列中才会出现第一类Stirling数。
    3. 在第一类Stirling数中，s(n,1)=n! ，也即左起第n个三角形最底端的那个数等于n!。从上面的第二个性质来看，这也是显然的。
    4. O(n^3)的算法实际上就是在绘制上面这个图。每一次j循环末，我们得到
的序列是第i个三角形中每一行左起第j个数组成的序列。例如，计算第5个三角形内的数时，程序首先累加出1, 11, 46, 96, 120, 120，这样便算出了a[5]=120，数列的前5个数再次累加即得到1, 12, 58, 154, 274，由此算出a[4]=274。
    第二个性质可以利用第一个性质进行数学归纳法证明，证明很简单，我就不多说了。现在我尽可能少写一些繁琐的细节，节约一些时间用来复习古代汉语。

做人要厚道，
转贴请注明出处。

查看更多：
http://www.luschny.de/math/factorial/FastFactorialFunctions.htm
http://www.luschny.de/math/factorial/index.html <—- 巨牛，20多种阶乘算法的代码！

KMP算法与一个经典概率问题

/ 22 条评论

    考虑一个事件，它有两种概率均等的结果。比如掷硬币，出现正面和反面的机会是相等的。现在我们希望知道，如果我不断抛掷硬币，需要多长时间才能得到一个特定的序列。

序列一：反面、正面、反面
序列二：反面、正面、正面

    首先，我反复抛掷硬币，直到最近的三次抛掷结果形成序列一，然后我记下这次我抛掷了多少次才得到了我要的序列。重复执行这个过程，我可以算出得到序列一平均需要的抛掷次数。同样地，反复抛掷硬币直到序列二产生，它所需要的次数也有一个平均值。你认为这两个平均值哪一个大哪一个小？换句话说，出现序列一平均所需的抛掷次数少还是出现序列二平均需要的次数少？

    大多数人会认为，两个序列会以同样快的速度出现，因为在所有“正”和“反”的8种三元组合里，“反正反”和“反正正”各占1/8，其概率是均等的。而事实上，我们将会看到掷出序列二所需的次数更少一些。不妨考虑这样一个问题：在由“正”和“反”构成的n位01序列中，有多少个序列以序列一结尾但之前不曾出现过序列一？有多少个序列以序列二结尾但之前不曾出现过序列二？当n比较小时，两者答案是一样的（例如n=3时符合要求的情况都是唯一的），但到后来n越大时，两者的差距越明显：后者的个数总比前者的个数要多一些。不妨看一看n=6的情况。对于序列一，只有以下5个序列是符合要求的：

  • 反反反反正反
  • 反正正反正反
  • 正正正反正反
  • 正反反反正反
  • 正正反反正反

    但对于序列二来说，符合条件的序列就有7个：

  • 反反反反正正
  • 反正反反正正
  • 反反正反正正
  • 正反反反正正
  • 正正反反正正
  • 正正正反正正
  • 正反正反正正

    你可以通过计算机编程枚举，计算一下n为其它值的情况。计算结果和刚才也一样：在n位01序列中，以序列二结尾但之前不含序列二的情况不会少于以序列一结尾但之前不含序列一的情况。这说明，抛掷第n次硬币后恰好出现了序列二，其概率不会小于恰好出现序列一的概率。显然，当n渐渐增大时，这个概率应该呈下降趋势；同时，随着n的增长，两个序列各自出现的概率由相等开始慢慢拉开差距，第n次抛掷产生序列二的概率下降得要缓慢一些，或者说更多的情况集中发生在n更小的时候。因此总的来说，出现序列二所需要的抛掷硬币次数的期望值更小。
    虽然我们通过一系列的观察验证了这个结论，并且我们也相信这个结论是正确的（虽然没有严格的证明），但我们仍然不是很接受这个结论。这种情况是有悖于我们的直觉的，它与我们的生活经验不相符合。此刻，我们迫切需要一个解释，来说明这种出人意料的反常现象产生的原因。

    如果不亲自做几次试验的话，你很难体会到这种微妙的差距。考虑整个游戏的实际过程，“反正正”序列显然会出现得更早一些。假如某一次我们得到了序列“反正”。如果我们需要的是“反正反”序列，那么下一次抛掷结果为反面将结束本轮的抛掷，而下一次是正面则前功尽弃，你必须再次从零开始。如果我们需要的是“反正正”序列，那么下一次抛掷结果为正面将结束本轮的抛掷，而下一次是反面的话我至少不会惨到一切归零，这相当于我已经有了一个反面作为新的开头，只需再来两个正面即可。这样看的话，提前掷出“反正正”的可能性更大一些。
    反复体会上面的想法，了解KMP算法的网友会恍然大悟：这就是KMP算法的基本思路！考虑这样一个问题：我们在当前字串中寻找子串“反正正”第一次出现的位置。假如当前已经能匹配模式串的前两个字“反正”，主串中的下一个字是“正”则匹配成功，主串的下一个字是“反”则将使模式串的当前匹配位置退到第一个字。考虑一个更复杂的例子：我们希望在主串中寻找子串abbaba，现在已经在主串中找到了abbab。如果主串下一个字符是a，则成功匹配；如果主串下一个字符是b，则模式串最多能匹配到的位置退到了第三个字符，我只需要从abb开始继续匹配，而不必一切从头再来。
    我们可以用KMP算法完美地解决上面的问题。首先预处理出一个数组c，c[i,0]表示模式串匹配到了第i个字符，主串下一个字符为0（反）时，模式串的匹配位置将退到哪里；同样地，c[i,1]表示模式串匹配到了第i个字符，主串下一个字符为1（正）时，新的模式串匹配位置在什么地方。设f[i,j]表示第i次抛掷硬币后恰好匹配到模式串第j位有多少种情况，则f[i,j]=Σf(i-1,k) + Σf(i-1,l)，其中k满足c[k,0]=j，l满足c[l,1]=j。将f[i,j]除以2的i次方，我们就得到了相应的概率值。或者更直接地，设P[i,j]表示第i次抛掷硬币后，最远能匹配到的模式串位置是第j位的概率，则P[i,j]=Σ( P(i-1,k)/2 ) + Σ( P(i-1,l)/2 )。注意，我们还应该添加一种特殊的概率值P[i,*]，它表示在主串第i个字符以前已经成功匹配过的概率，这样的话下表中每一列的和才能为1。

    来看一看程序的输出结果：
Pattern 1: s[]="aba"
主串位置       1        2       3       4       5       6       7       8       9      10
匹配到s[0]  0.5000  0.2500  0.2500  0.2500  0.2188  0.1875  0.1641  0.1445  0.1270  0.1113
匹配到s[1]  0.5000  0.5000  0.3750  0.3125  0.2813  0.2500  0.2188  0.1914  0.1680  0.1475
匹配到s[2]  0.0000  0.2500  0.2500  0.1875  0.1563  0.1406  0.1250  0.1094  0.0957  0.0840
匹配到s[3]  0.0000  0.0000  0.1250  0.1250  0.0938  0.0781  0.0703  0.0625  0.0547  0.0479
已找到匹配  0.0000  0.0000  0.0000  0.1250  0.2500  0.3438  0.4219  0.4922  0.5547  0.6094

Pattern 2: s[]="abb"
主串位置       1        2       3       4       5       6       7       8       9      10
匹配到s[0]  0.5000  0.2500  0.1250  0.0625  0.0313  0.0156  0.0078  0.
0039  0.0020  0.0010
匹配到s[1]  0.5000  0.5000  0.5000  0.4375  0.3750  0.3125  0.2578  0.2109  0.1719  0.1396
匹配到s[2]  0.0000  0.2500  0.2500  0.2500  0.2188  0.1875  0.1563  0.1289  0.1055  0.0859
匹配到s[3]  0.0000  0.0000  0.1250  0.1250  0.1250  0.1094  0.0938  0.0781  0.0645  0.0527
已找到匹配  0.0000  0.0000  0.0000  0.1250  0.2500  0.3750  0.4844  0.5781  0.6563  0.7207

    这下我们可以清楚地看到，序列二提前出现的概率要大得多。注意到，根据我们的概率定义，表格中每一列的数字之和都是1。同时，倒数第二行的数字之和（有无穷多项）也应该为1，因为最后一行的概率就是倒数第二行的概率值累加的结果，而根据最后一行概率的定义，主串无穷长时已找到匹配的概率应该为1。因此，我们也可以把倒数第二行看作是模式串在主串第i个位置首次匹配成功的概率。我们可以根据这一结果近似地计算出抛掷次数的期望值。

Matrix67原创
转贴请注明出处

趣题：用最简单的话来描述一个集合

/ 5 条评论

    定义f(n)的值为将n拆分成若干个2的幂的和，且其中每个数字出现的次数不会超过两次的方案数。规定f(0)=1。
    例如，有5种合法的方案可以拆分数字10：1+1+8, 1+1+4+4, 1+1+2+2+4, 2+4+4 和 2+8。因此，f(10)=5。
    请用一句最简单的话来描述集合{ f(n)/f(n-1) }。证明你的结论。

    注意：答案远比一个递归公式来得精辟，来得巧妙。如果你发现了我们的结论，你会一眼认定它为正确答案。

    答案：数列{ f(n)/f(n-1) }以最简形式包含了所有的正有理数。

    如果n是奇数（等于2m+1），那么数字1（即2^0）必须出现且只能出现一次。现在的问题就是，2m的拆分方案中有多少个方案不含数字1呢？稍作思考你会立即发现，它就等于f(m)，因为m的所有拆分方案的所有数都乘以2后正好与不含1的2m拆分方案一一对应。因此，f(2m+1) = f(m)
    如果n是偶数（等于2m），那么数字1要么没有出现，要么恰好出现两次。对于前一种情况，我们有f(m)种可能的方案；第二种情况则有f(m-1)种方案。因此，f(2m) = f(m) + f(m-1)
    另外，显然f(k)都是正数。于是，f(2k-1) = f(k-1) < f(k-1)+f(k) = f(2k)
    这样，我们可以得到以下三个结论：

    结论1：gcd( f(n),f(n-1) ) = 1
    证明：对n进行数学归纳。显然gcd( f(1),f(0) ) = gcd(1,1) = 1
    假设对于所有小于n的数结论都成立。根据n的奇偶性，下面两式中必有一个成立：
    gcd( f(n),f(n-1) ) = gcd( f(2m+1),f(2m) ) = gcd( f(m), f(m)+f(m-1) ) = gcd( f(m),f(m-1) ) = 1
    gcd( f(n),f(n-1) ) = gcd( f(2m),f(2m-1) ) = gcd( f(m)+f(m-1), f(m-1) ) = gcd( f(m),f(m-1) ) = 1

    结论2：如果f(n+1)/f(n) = f(n'+1)/f(n')，那么n=n'
    证明：还是数学归纳法。当max(n,n')=0时结论显然成立，因为此时n=n'=0。
    假如对于所有小于n的数结论都成立。由于f(2k-1)<f(2k)，那么要想f(n)/f(n-1) = f(n')/f(n'-1)，n与n'的奇偶性必须相同，于是可以推出f(m)/f(m-1) = f(m')/f(m'-1)，根据归纳我们有m=m'，这就告诉我们n=n'。

    结论3：对于任何一个有理数r，总存在一个正整数n使得r=f(n)/f(n-1)。
    证明：把r写成两个互素的数p和q的比。我们对max(p,q)施归纳。
    显然，当p=q=1时结论成立，此时n=1。
    不妨设p<q，那么定义r'为p/(q-p)。根据归纳假设，总存在一个数m满足r'=f(m)/f(m-1)。于是r=f(2m+1)/f(2m)。当p>q时同理可证明。

做人要厚道
转贴请注明出处

魔方问题新进展：26步足以破解任何魔方

/ 18 条评论

    最近，波士顿Northeastern大学的计算机科学家Daniel Kunkle证明了任何一个魔方可以在26步以内解开。这个结果打破了以往所有的记录。在解魔方的处理过程中，他构造了一些非常具有启发性的算法，这篇文章将简单地介绍一下这些算法。
    一个魔方大约有4.3 x 10^19种可能的初始状态，再牛的机器也不可能搜索完所有的可能。因此Kunkle和他的指导员Gene Cooperman想出了一些对魔方状态进行分类筛选的策略。
    Kunkle和Cooperman首先运用了一个小技巧将问题进行简化。如果魔方的每个面全是一种颜色，我们就认为魔方被解开，不管哪一面是哪一种颜色。换句话说，相互之间可以通过颜色置换得到的初始状态都是等价的。这样，“本质不同”的初始状态就减少到10^18种。
    接下来，他们开始观察一类更简单的问题：如果只允许180度转动(half-turn)，有多少状态可以被解决。在10^18种状态中，只有大约15000种状态可以仅用180度旋转来破解。对于普通计算机来说，这个数目也不大，只需要不到一天的时间就可以搜索出解开所有15000多个魔方各自需要的最少步数。他们发现，这类初始状态中任何一个都可以在13步以内解决。
    然后他们需要做的就是找出，需要多少步才能把任意一种状态转化为这15000种特殊状态中的一个。为了完成这一工作，首先他们把所有的初始状态划分为若干个等价类，每个等价类里的状态都可以仅用180度转动互相得到。这样，同一个等价类中如果任一状态可以变换为其中一种特殊状态，同样的转动步骤也可以使该等价类的其它所有状态都变成特殊状态。最后他们找到了1.4 x 10^12个不同的等价类，需要解决的状态数由最初的4.3×10^19减少到1.4×10^12。但无论如何，10^12仍然是一个恐怖的数字。
    现在他们用了一台超级计算机来完成这个工作，并且使用了一些很有技巧性的决策来加速搜索过程。计算机需要耗费大量的时间读取硬盘上的数据，为了加快速度，Kunkle和Cooperman将数据巧妙地进行了处理，使得数据的排列正好与计算机读取的顺序相符，这样就节省了搜索硬盘的时间。
    “这种方法可以应用在任何一个组合问题上”，Kunkle说。他提到了西洋跳棋、国际象棋、航班安排和蛋白质摺叠等一系列问题。一种类似的组合学方法最近被用于寻找西洋跳棋的最优策略中。
    63小时的计算后，超级计算机得到的答案是，任何一种状态都能在16步以内转化为15000种特殊状态。而这些特殊状态又只需要13步达到最终状态，因此这种方法最终得到的结论是：29步以内可以解决任何一个魔方问题。
    但这个数字还不足以创造出新的记录，去年瑞典就曾经得到过27步内解决魔方问题的结论。Kunkle和Cooperman意识到，要想打破这个记录，他们还需要削减3步才行。
    应用他们现有的算法，只有8×10^7个状态集合还不能做到26步以内出解。再次对这些相对较少的状态进行搜索，最终他们找到了26步以内解决所有魔方的方法。
    7月29日他们在ISSAC(International Symposium on Symbolic and Algebraic Computation,国际符号和代数计算会议)上公布了这一结果。
    现在Kunkle和Cooperman希望把最大步骤数减少到25。他们认为他们可以对所有需要26步的状态进行暴力搜索来寻找更优的方案。
    虽然他们已经获得了很大的成功，但这一结果很可能还有改进的空间。许多学者认为20步以内足以解决任何魔方，但现在没有人能够证明。

Matrix67翻译，原文地址
做人要厚道，转贴请注明出处

OI/MO必备：巨牛无比的公式、定理速查表

/ 20 条评论

    数学考试时我最怕的就是三角函数，几十个公式我一个都背不到。那时我有了制作公式定理表的想法。经过反复尝试，我那张表已经设计得非常合理了，表里的内容也初具规模。我复印了几份给我的几个同学，反映都还不错，其它的同学听说了都想来找我要一份。当初我以为我那张表已经很牛了，今天终于发现我错了。
    刚才偶然发现一份非常牛的公式定理表，满满写了10页，不但包含有完整的三角公式、微分表、积分表，还有排列组合公式、概率公式、质数表、杨辉三角等等，甚至还有主定理、图论概念等东西。想要公式定理手册的OI/MO牛不用再去买中学数理化的口袋书了，你真正需要的东西那上面根本没有；这10页的速查表才是真正为你设计的，打印一份随身携带更能体现你nerd/geek的身份……
    点击这里下载(pdf, 154KB) 请勿直接链接到此文件