想必搞OI/ACM的朋友都应该知道八皇后问题，这是学习编程的必修课程之一：在国际象棋棋盘上最多可以放置多少个互不攻击的皇后（皇后可以攻击它所在的行、列、对角线方向上的棋子）？显然，能够放置的皇后数不超过8个，因为国际象棋的棋盘一共就8行8列。事实上，放置8个互不攻击的皇后是有可能的，并且方法不止一种。
    上个月的IBM Ponder This考虑了一个八皇后问题的扩展：最多可以在国际象棋棋盘上放置多少个皇后，使得每一个皇后最多只能攻击到一个其它的皇后？

Read more…

  
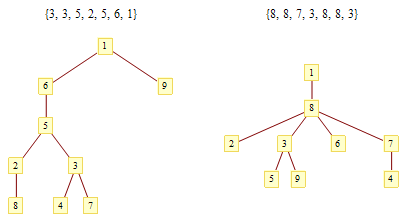
    Cayley公式是说，一个完全图K_n有n^(n-2)棵生成树，换句话说n个节点的带标号的无根树有n^(n-2)个。今天我学到了Cayley公式的一个非常简单的证明，证明依赖于Prüfer编码，它是对带标号无根树的一种编码方式。
    给定一棵带标号的无根树，找出编号最小的叶子节点，写下与它相邻的节点的编号，然后删掉这个叶子节点。反复执行这个操作直到只剩两个节点为止。由于节点数n>2的树总存在叶子节点，因此一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。下面我们只需要说明，任何一个长为n-2、取值范围在1到n之间的数列都唯一地对应了一棵n个节点的无根树，这样我们的带标号无根树就和Prüfer编码之间形成一一对应的关系，Cayley公式便不证自明了。
Read more…

    IMO 2001第三题：21个女生和21个男生一起参加了一场数学竞赛。结果显示，每个参赛者最多做对了6道题，并且对于任一对男生和女生，至少有一道他们都做对了的题。
    求证：存在这样的一道题，至少有三个女生和三个男生同时做对。

    当然，这个题目背景无趣而又生硬。如果是我的话，我肯定会把题目改成下面这个样子：21个女生和21个男生参加速配游戏，每个人独立地在自己的纸上写下不超过6种兴趣爱好。结果显示，对于任一对男女，他们都写下了至少一个相同的爱好。求证，存在某一个兴趣爱好，有至少三男三女都把它写上了。

    我是一个忠实于原题的好娃娃，因此还是用数学竞赛来当题目背景。对于每个问题，如果有至少3个男生答对了，就给这个问题添加一个标记“B”；如果有至少3个女生答对了，就给这个问题添加一个标记“G”。然后我们画一张21×21的表格，横行代表男生，纵列代表女生。每一个格子都代表一道对应的男女同时做对的题（不同的格子可能对应相同的题目），我们把对应的题目的“B”、“G”标记填进格子里。
    下面我们说明，每一横行里至少有11个格子标了“G”，每一个纵列里至少有11个格子标了“B”。考虑某一个特定的人，他（她）与每一个异性参赛者都有同时答对的题目，但他（她）自己最多只做出6道题。这6道题目需要“分配”给21个异性参赛者。我们希望知道最多有多少道题被不超过2个异性参赛者答对。显然，最极端的情况就是其中的5道题目每道分别被2个异性做对，剩下的第6道题被其余11个异性做对。反过来这也就是被至少三个人答对的题目最少的情况，因此每一行（列）里都有至少11个格子标有异性的标记。
    这样，我们就有了至少21*11个标有“G”的格子，和至少21*11个标有“B”的格子。但21*11*2 > 21*21，因此总有一个格子被同时标上了“G”和“B”。

来源：http://www.cut-the-knot.org/pigeonhole/BoysGirlsProblems.shtml

    最近，Claudio Baiocchi提出了这样一个问题：用相同形状的多联骨牌拼成完全对称图形，问对于哪些多联骨牌问题是有解的。这个问题最早出现在Erich Friedman今年一月的Math Magic里。令人吃惊的是，所有不超过6联的骨牌都是有解的。Erich Friedman自己找到了大多数的解，Corey Plover也找出了一些解，其余的解则是George Sicherman发现的。
    单联到6联的骨牌个数分别为1, 1, 2, 5, 12, 35。它们的解分别如下：

Monomino:

Domino:

Trominoes: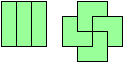

Tetrominoes: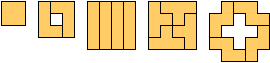

Pentominoes: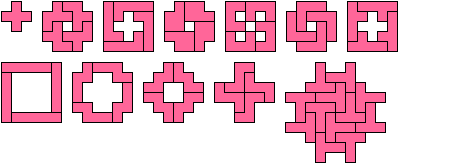

Hexominoes:

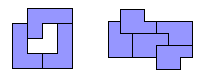    由单位正方形拼接而成的图形叫做多联骨牌(Polyomino)。一个有趣的问题是，能否用奇数个相同的多联骨牌拼成一个对称图形？答案是肯定的。右图显示了如何用奇数个相同的多联骨牌拼接出中心对称图形和沿对角线方向轴对称的图形。
    下面的问题该轮到你来回答了。你能否用奇数个相同的多联骨牌拼接出一个左右轴对称的图形？当然，你所使用的多联骨牌本身必须是不对称的。为了方便起见，下文我们所说的“轴对称”均不再考虑沿对角线方向对称的情况。
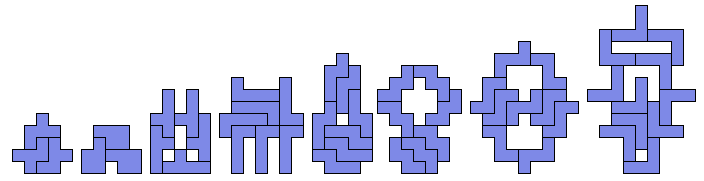
    五联骨牌共有12种。令人吃惊的是，对于上述问题，所有这12种骨牌都有至少一个解。其中长条形、十字架形、T字形和U字形这4种是本来就对称的。你能否找出其余8种五联骨牌的解？
    并非所有的多联骨牌都是有解的，有一些六联骨牌就没有解。你能否找出一个没有解的多联骨牌，并证明它确实不可能有解？

    其实，用奇数个相同的多联骨牌拼出左右轴对称的图形是完全有可能的，并且这样的情况非常之多。下面随便举几个例子。你刚才都想到了哪些？
  

    对于这个问题，8种非对称的五联骨牌都是有解的。下面就是这8个图形的解：
  

    下面我们证明，你永远不可能用奇数个h形六联骨牌排成一个左右轴对称的图形。
  
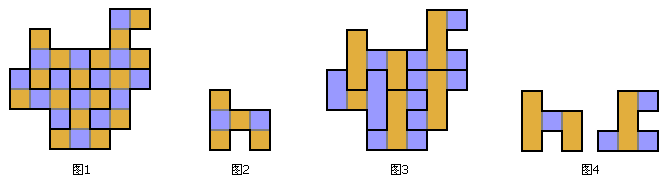
    像国际象棋棋盘一样对拼出来的图形进行染色（图1），你会发现同一块h形骨牌里两种颜色的格子数量始终不等（图2），奇数个骨牌加起来两种颜色的总格子数目显然也就不会相等；但一个沿格子边线轴对称的图形，两种颜色的格子应该一样多才对。现在的问题是，如果对称轴在格子内的中心线上咋办。为此，我们还需要对拼出来的图形进行带状染色（图3）。注意到不管这些骨牌怎么放，同一个骨牌中每种颜色的格子都是奇数个（图4），奇数个骨牌加起来，每种颜色的格子总数也都还是奇数个。而在拼接出来的图形里，对称轴所在的那些格子全是一种颜色，另一种颜色的格子则左右对称分布，这种颜色的格子数应该有偶数个才对。这样我们就证明了，用奇数个h形六联骨牌不能拼出轴对称的图形。

更多的结论可以在这里看到：http://www.monmouth.com/%7Ecolonel/oddities/index.html