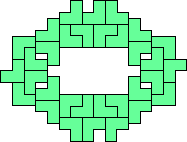
这是一个由“L”形三联骨牌拼成的图形。你能看出这个图形有什么神奇的地方吗?
答案:每一个“L”形板块都与另外四个“L”相邻。这是目前已知的满足这种性质的最小构造。“中心对称”并不是我们想要的答案。我们能用“L”形骨牌轻易构造出大量满足中心对称的简单图形来。

这是一个由“L”形三联骨牌拼成的图形。你能看出这个图形有什么神奇的地方吗?
答案:每一个“L”形板块都与另外四个“L”相邻。这是目前已知的满足这种性质的最小构造。“中心对称”并不是我们想要的答案。我们能用“L”形骨牌轻易构造出大量满足中心对称的简单图形来。
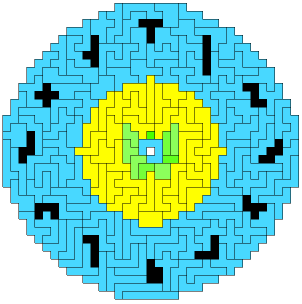
由n个单位正方形拼接而成的图形叫做n联骨牌。一联骨牌和二联骨牌显然都只有一种。三联的有两种(长条形和拐角形)。四联、五联、六联和七联骨牌则分别有5种、12种、35种、108种。有牛人竟然把所有这些多联骨牌拼成了一个圆形,更神的是12个五联骨牌的位置让整个圆盘变成了一个钟表的盘面!这12个五联骨牌正好分布在圆盘周围12个间距相当的地方,其中5和10的位置分别用罗马数字V和X表示,9和12则用英文首字母N和T表示。圆盘中间是一联、二联、三联、四联骨牌,外围是35个六联骨牌,再外面则是107个七联骨牌。第108个七联骨牌——中间有一个空洞的特殊骨牌——则被放在了整个圆盘的正中间。
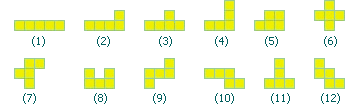
IBM Ponder This上个月的题目:一个多联骨牌(polyomino)是指平面上若干个正方形相接拼成的图形。经过旋转、镜像得到的图形仍然视为相同的多联骨牌。如上图所示,五联骨牌一共有12种。我们说一个多联骨牌A覆盖B,如果我们能在B上添加若干个新的方块得到A。回答下面两个问题:
1. 一个六联骨牌最多可以覆盖多少种不同的五联骨牌?
2. 给出一个最小的能够覆盖所有12种五联骨牌的图形。
最近,Claudio Baiocchi提出了这样一个问题:用相同形状的多联骨牌拼成完全对称图形,问对于哪些多联骨牌问题是有解的。这个问题最早出现在Erich Friedman今年一月的Math Magic里。令人吃惊的是,所有不超过6联的骨牌都是有解的。Erich Friedman自己找到了大多数的解,Corey Plover也找出了一些解,其余的解则是George Sicherman发现的。
单联到6联的骨牌个数分别为1, 1, 2, 5, 12, 35。它们的解分别如下:
Monomino:
Domino:
Trominoes: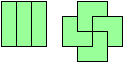
Tetrominoes: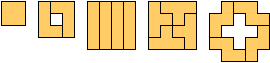
Pentominoes: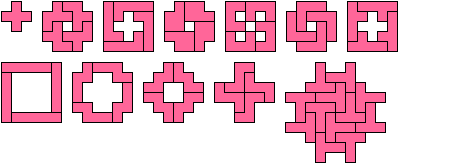
Hexominoes:
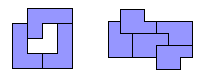 由单位正方形拼接而成的图形叫做多联骨牌(Polyomino)。一个有趣的问题是,能否用奇数个相同的多联骨牌拼成一个对称图形?答案是肯定的。右图显示了如何用奇数个相同的多联骨牌拼接出中心对称图形和沿对角线方向轴对称的图形。
由单位正方形拼接而成的图形叫做多联骨牌(Polyomino)。一个有趣的问题是,能否用奇数个相同的多联骨牌拼成一个对称图形?答案是肯定的。右图显示了如何用奇数个相同的多联骨牌拼接出中心对称图形和沿对角线方向轴对称的图形。
下面的问题该轮到你来回答了。你能否用奇数个相同的多联骨牌拼接出一个左右轴对称的图形?当然,你所使用的多联骨牌本身必须是不对称的。为了方便起见,下文我们所说的“轴对称”均不再考虑沿对角线方向对称的情况。
五联骨牌共有12种。令人吃惊的是,对于上述问题,所有这12种骨牌都有至少一个解。其中长条形、十字架形、T字形和U字形这4种是本来就对称的。你能否找出其余8种五联骨牌的解?
并非所有的多联骨牌都是有解的,有一些六联骨牌就没有解。你能否找出一个没有解的多联骨牌,并证明它确实不可能有解?
其实,用奇数个相同的多联骨牌拼出左右轴对称的图形是完全有可能的,并且这样的情况非常之多。下面随便举几个例子。你刚才都想到了哪些?

对于这个问题,8种非对称的五联骨牌都是有解的。下面就是这8个图形的解:
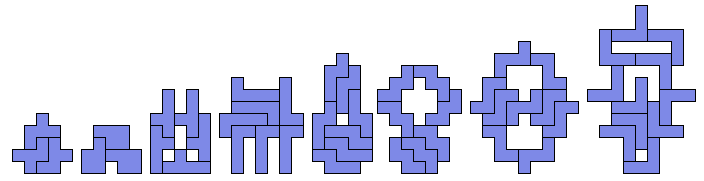
下面我们证明,你永远不可能用奇数个h形六联骨牌排成一个左右轴对称的图形。
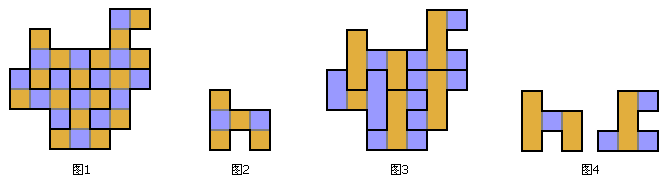
像国际象棋棋盘一样对拼出来的图形进行染色(图1),你会发现同一块h形骨牌里两种颜色的格子数量始终不等(图2),奇数个骨牌加起来两种颜色的总格子数目显然也就不会相等;但一个沿格子边线轴对称的图形,两种颜色的格子应该一样多才对。现在的问题是,如果对称轴在格子内的中心线上咋办。为此,我们还需要对拼出来的图形进行带状染色(图3)。注意到不管这些骨牌怎么放,同一个骨牌中每种颜色的格子都是奇数个(图4),奇数个骨牌加起来,每种颜色的格子总数也都还是奇数个。而在拼接出来的图形里,对称轴所在的那些格子全是一种颜色,另一种颜色的格子则左右对称分布,这种颜色的格子数应该有偶数个才对。这样我们就证明了,用奇数个h形六联骨牌不能拼出轴对称的图形。
更多的结论可以在这里看到:http://www.monmouth.com/%7Ecolonel/oddities/index.html