最近在reddit上看到了这么一个有趣的问题：下图是一个单位立方体，黑色实线分别是立方体相邻两个面的两条对角线。你觉得这两条对角线之间的最短距离是多少？
可以提前告诉你，答案不是√2/2。
图形
Image Functions：在线绘制颜色分布图
Image Functions是最近web 2.0上谈论很多的一个在线小程序。你可以在输入框里输入一个关于x、y、r、g、b的函数，系统将给出对应的图像并储存在画册里。你可以试着输入0.2*(x+y)或者sin(x)*cos(y)试试。没事可以点随机查看，偶尔你将会看到一些牛人绘制的牛图：
floor(3/(x*x*50+(y+6)**2+1))+floor(1/((x-2)**2+(y+9)**2*80+1))+floor(1.4/((y+2.8)**2*0.1+x*x*0.04+0.01))-3/(x*x+(y+1.0)**2*180)+floor(2/((y-3)**2*0.2+0.5*(abs(x)-3.5)**2*2+0.1))+floor(2.8/((y+5)**2*1.5+0.5*(abs(x)-5)**2*2.5+0.1))+floor(1.6/((y-4)**2*0.03+x*x*0.1+0.1))+floor(1.5/((y-10)**2+0.5*(abs(x)-3)**2))-floor(9/((y+3)**2*2.4+(abs(x)-1.9)**2*2.4))+floor(2.8/((y+9)**2*1.5+0.5*(x-4)**2*2.5+0.1))
这个图形有什么牛B的地方？
圆环面积公式与勾股定理
勾股定理有上百种证明，但其实它们都大同小异——无非是构造一组三角形和正方形并进行一系列变换。今天我看到了一个用圆面积来解释勾股定理的办法，颇有一些新意。
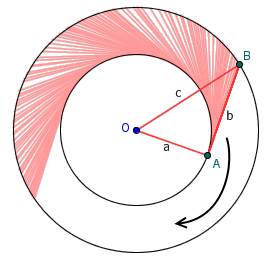
考虑直角三角形OAB绕着一个锐角顶点O旋转一周。顶点A的轨迹是一个半径为a的圆，顶点B的轨迹是一个半径为c的圆。那么，线段AB扫过的区域（一个圆环）的面积就应该是大圆面积减去小圆面积，即π(c^2-a^2)。如果我们能够有一种办法说明，线段AB扫过的面积正好是πb^2，我们就相当于得到了勾股定理的另一个证明。
网友来信：另类线段等分法与距离平方和问题的扩展
在介绍尺规作图等分圆面积时，我提到了利用尺规作图将线段AB任意等分的问题。在初中课本上，这个问题的标准做法如下：
1. 过A点向另一方向做射线l；
2. 从A点开始，用圆规在射线l上截取n个等距的点X1, X2, …, Xn；
3. 连接Xn和B；
4. 分别过X1, X2, …, Xn-1作直线平行于XnB。
那么，这些平行线与AB的交点即为AB的n等分点。