国外有人发现一个鲜为人知的古董级函数作图软件—— GrafEq 。这个软件只有 2M 大小,它的功能就只有一个:作出形如 x2 + y2 = 1 的二元等式或者不等式的图像。令人惊叹的是,这个软件的图像绘制能力异常强大, Mathematica 等大型专业数学软件完全不是它的对手。
这个软件早就没再更新了。它的“最新版本”是 2.12 ,只支持 Windows 95 到 Windows XP 的系统,或者 PowerPC 7.12 到 MacOS 9.2 的系统,可见其年代久远。神奇的是,这个软件的官方网站依然健在,而且软件竟然也都能下载。如果你有幸还能装上这款软件,你将有机会重温一次 Windows 95 时代的软件安装画面。
图形
锈规作图续篇:单用一个只能画单位圆的圆规如何作线段中点
在这个 Blog 的一篇很老很老的文章里,我曾经讲过一个非常有趣的几何作图问题,这个问题最早是由 D. Pedoe 教授在 1983 年提出的:给定 A 、 B 两点,只用一个生锈的圆规(没有直尺),如何找出一个点 C ,使得 A 、 B 、 C 恰好构成一个等边三角形?所谓“生锈的圆规”,也就是一个被卡住的圆规,它的两脚张角不能改变。我们不妨假设,它只能画出单位大小的圆。1987 年,我国的侯晓荣等人成功地解决了这个问题,并借助复平面理论得到了很多一般的结果,其研究成果《锈规作图论》发表在了《中国科学技术大学学报》上。
锈规作出等边三角形的方法非常漂亮:利用锈规作图,我们能构造出两点之间由单位长线段构成的折线段,进而实现平行四边形的构造(已知其中三个点,能够只用锈规找出第四个点),进而完成等边三角形的构造。刚才提到的那篇“很老很老的文章”里有详细的描述,继续阅读之前,强烈建议先看一看。
事实上,D. Pedoe 教授还提过另外一个问题:给定 A 、 B 两点,只用锈规能否作出 A 、 B 连线的中点?注意,由于没有直尺,线段 AB 实际上是画不出的。要想“隔空”找出线段的中点,显然并不容易。
前几天翻起张景中的《数学家的眼光》,就是为了查阅这个问题的解决方法。《数学家的眼光》一书中详细描述了锈规作图找中点的方法,在这里和大家分享。
视频:How Round is Your Circle 各种神奇的几何构造
这是今天在 MathPuzzle 上看到的视频。视频里演示了单平衡多面体、Peaucellier 连杆等非常帅气的几何图形和机械系统的实物版。这些几何构造各显神通,来头都不小,都是非常不错的数学话题。
大家看完这个视频后的感觉估计会跟我一样:为什么没有 Gömböc 呢?
比Conway生命游戏更酷的Langton蚂蚁
不知道有多少人已经熟知 Conway 的生命游戏,但却从没听说过 Langton 的蚂蚁游戏?反正我是其中之一。直到今天我才听说了这个比生命游戏更酷的游戏—— Langton 的蚂蚁。这也是一个二维自动机形式的零玩家游戏,不过我觉得它比生命游戏有趣得多。这有两个理由:
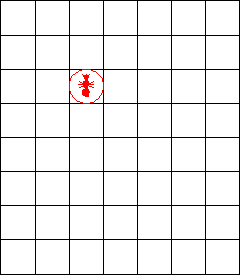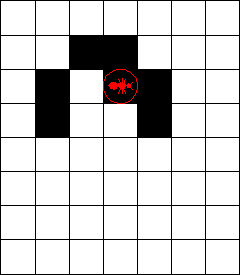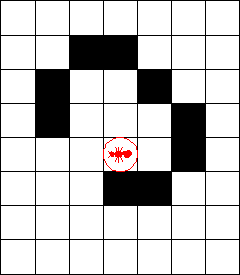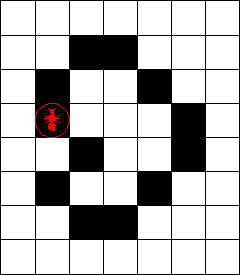
1. 它的算法过程更简单。初始时,蚂蚁位于一张空白画布的某个方格里。如果当前蚂蚁在白色方格上,则对当前方格反色,左转 90 度,前进一格;如果当前蚂蚁在黑色方格上,则对当前方格反色,右转 90 度,前进一格。如此反复。
漫话折纸几何学
前几天,一篇叫做 用正方形纸片折出等边三角形 的日志引起大家的讨论,折出正七边形和折出角三等分线的方案更是让大家争论不休。提得最多的问题就是,折纸为什么要比尺规作图更强?这是一个好问题。我查了不少资料,了解到不少折纸几何的历史,收获颇大,不赶紧记下来就亏大了。于是有了这篇文章。
要解答为何折纸如此强大,首先我们得解决一个问题:什么叫折纸。折纸的游戏规则是什么?换句话说,折纸允许哪些基本的操作?大家或许会想到一些折纸几何必须遵守的规则:所有直线都由折痕或者纸张边缘确定,所有点都由直线的交点确定,折痕一律是将纸张折叠压平再展开后得到的,每次折叠都要求对齐某些已有几何元素(不能凭感觉乱折),等等。不过,这些定义都太“空”了,我们需要更加形式化的折纸规则。 1991 年, Humiaki Huzita 指出了折纸过程中的 6 种基本操作(也可以叫做折纸几何的公理):
1. 已知 A 、 B 两点,可以折出一条经过 A 、 B 的折痕
