有 1000 枚硬币堆在一起。把它们任意分成两堆,并计算出这两堆的硬币数的乘积。然后,任意选择其中的一堆硬币,把它继续分成两个更小的堆,并计算出这两堆的硬币数的乘积。不断这样做下去,直到最后每堆都只剩一枚硬币为止。求证:把途中产生的所有乘积全部加在一起,结果是一个定值,它不随分法的改变而改变。
图形
趣题:构造更大的Brunnian link
下图中的三个绳圈套在一起,没有哪一个绳圈能从中分离出来。不过,真正有趣的是,如果去掉其中任意一个绳圈,那么其他所有的绳圈都全部散开了。如果 n 个绳圈套在一起,并且任意去掉其中一个绳圈都会同时解开其他所有套着的绳圈,我们就把它叫做 n-component Brunnian link 。
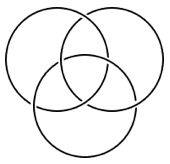
你能想出一个 n = 4 的 Brunnian link 吗? n = 5 呢? n 可以任意大吗?
趣题:把矩形分割为面积相同但形状各不相同的小矩形
Using your Head is Permitted 数学谜题站的主持人 Michael Brand 某日收到了来自 R. Nandakumar 的一个谜题:是否有可能把一个矩形剖分成若干个小矩形,使得每个小矩形的形状互不相同,但它们的面积都一样?没有想到,从这个问题出发,加上一些非常机智巧妙的分析与构造,我们能得到越来越多有意思的东西。于是,它就变成了 Using your Head is Permitted 今年 3 月的谜题。看了谜题的答案后,我也被彻底折服,决定把这一系列的思考重述在此,和大家一同分享。为了简便起见,下面的“矩形剖分方案”一律指的是把一个大矩形分割成若干个小矩形的方案。
无聊小制作:“数词+非数词+数词+非数词”的出现频数
昨天和同事聊到,汉语还真是奇怪,有“四分五裂”,有“五颜六色”,也有“七上八下”,但好像从没听说过六什么七什么的。于是想到,在汉语中,“数词 + 非数词 + 数词 + 非数词”的短语是怎样分布的呢?回到家后立即用 Mathematica 做了一个柱状图,绘出了九九八十一种数词短语模式在大规模真实语料中的出现频数。注意,这里统计的是总的出现频数,重复出现也会计算在内。另外,这是一个简单而机械的统计过程,因而 “三人一组”、“七天七夜”之类的非成语也被算了进来。

嗯,对,没有任何意义,纯属无聊之作。
数学冷知识:不断取英文表达的字符数,最后总会得到数字4
这道题的答案有几个字母?答案:four。
有趣的是,这是唯一的答案。如果令函数 f(n) 表示非负整数 n 的英文表达中有多少个字母(不算空格和短横线), n=4 是该函数的唯一不动点。
n 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
f(n) 4, 3, 3, 5, 4, 4, 3, 5, 5, 4, 3, …
事实上, @IanMathmogician 发现了一个更有趣的“数学冷知识”:任取一个 0 到 100 之间的整数 n ,算出这个数的英文表达中的字符个数,再算出所得结果的英文表达的字符数,并这样一直迭代下去,最后总会得到数字 4 。我用 Mathematica 做了一张图片,可以让大家直观地看到,这真的可以说是条条大路通向数字 4 啊。