图形
Borromean rings的另一个离奇的性质
下图中的图 (a) 是由三个绳圈组成的。这是一个非常经典的图形,叫做 Borromean rings 。 Borromean rings 有一个非常神奇的特点:它们是套在一起的,没有哪个绳圈能从中取出来;但是,仔细观察你会发现,每两个绳圈之间都并没有直接套在一起!
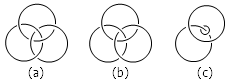
Borromean rings 还有一个听上去更离奇的性质:如图 (b) 所示,如果把其中任意两个绳圈真的套在一起,那么第三个绳圈就会自动脱落掉!为了看出这一点来,我们可以像图 (c) 那样,把其中一个绳圈缩小,让它紧紧地裹在另一个绳圈上,这下就很容易看出,它已经不再对第三个绳圈有任何限制作用了。
为什么Fibonacci数列相邻两项之比会趋于0.618?
你或许熟知一个非常经典的结论: Fibonacci 数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … (头两项都是 1 ,此后每一项都是前两项之和)的相邻两项之比将会越来越接近黄金比例 0.618 ,不信请看:
1 / 1 = 1.0000000…
1 / 2 = 0.50000000…
2 / 3 = 0.66666667…
3 / 5 = 0.60000000…
5 / 8 = 0.62500000…
8 / 13 = 0.61538462…
13 / 21 = 0.61904762…
21 / 34 = 0.61764706…
34 / 55 = 0.61818182…
55 / 89 = 0.61797753…
89 / 144 = 0.61805556…
144 / 233 = 0.61802575…
… …
Fibonacci 数列究竟是怎么和黄金比例扯上关系的?一个简单的解释就是,假设相邻两项之比存在一个极限,那么到了无穷远的时候,连续的三个数 a, b, a + b 将会满足 a / b = b / (a + b) ,这正好就是黄金比例的定义。我最近用 Mathematica 做了一组动画,尝试着用图形化的方法更直观地展示 Fibonacci 数列和黄金比例之间的联系。
Hofstadter的非线性递推数列
在著名奇书 Gödel, Escher, Bach: An Eternal Golden Braid 的第五章中,为了展现出递推序列的神奇之处,作者 Douglas Hofstadter 定义了这么一个递推序列: G(n) = n – G(G(n – 1)) ,其中 G(1) = 1 。这个序列的前 30 项如下:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| G(n) | 1 | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 6 | 6 | 7 | 8 | 8 | 9 | 9 | 10 | 11 | 11 | 12 | 12 | 13 | 14 | 14 | 15 | 16 | 16 | 17 | 17 | 18 | 19 |
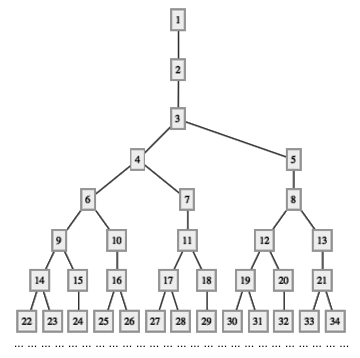
这个数列通常被称作 Hofstadter G-sequence 。它有什么特别的地方呢?如上图,如果把每个标号为 n 的结点都连接到标号为 G(n) 的结点下方,这样的话你将会得到一棵树。从第二行开始算起,各行的结点个数依次为 1, 1, 2, 3, 5, 8, 13, … 正好是著名的 Fibonacci 数列(头两个数都是 1 ,从第三个数开始,每个数都是前两个数之和)。如果我们把第 i 个 Fibonacci 数记作 Fi 的话,上面的规律可以重新表述为:当 n ≥ 2 时,这棵树的第 n 行的结点总个数为 Fn-1 。另外,这棵树的前 n 行的结点总数(也就是第 n 行最右边那个结点的编号)正好等于 Fn+1 ,也是一个个的 Fibonacci 数。对照上面两个事实,你会惊奇地发现,莫非 F1 + F2 + … + Fn-1 + 1 总是等于 Fn+1 ?事实的确如此,上面这个式子对于所有大于等于 2 的正整数 n 均成立。
五个有趣的拓扑变换问题
如果你喜欢上次的空间想象能力挑战,你一定会喜欢 V. V. Prasolov 的 Intuitive Topology 一书。书中的第一章有五个非常经典的“拓扑变换”类谜题,在此与大家分享。注意游戏规则:我们假设所有物体都是用橡胶做成的,可以随意地拉伸、挤压、弯曲,但不允许切断、粘连等任何改变图形本质结构的操作。
1. 能否把左图连续地变形为右图?

2. 能否把左图连续地变形为右图?
