虽然有些东西似乎是显然的，但一个完整的定义仍然很有必要。比如，大多数人并不知道函数的连续性是怎么定义的，虽然大家一直在用。有人可能会说，函数是不是连续的一看就知道了嘛，需要定义么。事实上，如果没有严格的定义，你很难把下面两个问题说清楚。
    你知道吗，除了常函数之外还存在其它没有最小正周期的周期函数。考虑一个这样的函数：它的定义域为全体实数，当x为有理数时f(x)=1，当x为无理数时f(x)=0。显然，任何有理数都是这个函数的一个最小正周期，因为一个有理数加有理数还是有理数，而一个无理数加有理数仍然是无理数。因此，该函数的最小正周期可以任意小。如果非要画出它的图象，大致看上去就是两根直线。请问这个函数是连续函数吗？如果把这个函数改一下，当x为无理数时f(x)=0，当x为有理数时f(x)=x，那新的函数是连续函数吗？
    Cauchy定义专门用来解决这一类问题，它严格地定义了函数的连续性。Cauchy定义是说，函数f在x=c处连续当且仅当对于一个任意小的正数ε，你总能找到一个正数δ使得对于定义域上的所有满足c-δ< x <c+δ的x都有f(c)-ε<f(x)<f(c)+ε。直观地说，如果函数上有一点P，对于任意小的ε，P点左右一定范围内的点与P的纵坐标之差均小于ε，那么函数在P点处连续。这样就保证了P点两旁的点与P无限接近，也就是我们常说的“连续”。这又被称作为Epsilon-Delta定义，可以写成“ε-δ定义”。
    有了Cauchy定义，回过头来看前面的问题，我们可以推出：第一个函数在任何一点都不连续，因为当ε< 1时，δ范围内总存在至少一个点跳出了ε的范围；第二个函数只在x=0处是连续的，因为此时不管ε是多少，只需要δ比ε小一点就可以满足ε-δ定义了。
    在拓扑学中，也有类似于ε-δ的连续性定义。假如一个函数f(t)对应空间中的点，对于任意小的正数ε，总能找到一个δ使得定义域(t-δ,t+δ)对应的所有点与f(t)的距离都不超过ε，那么我们就说f(t)所对应的曲线在点f(t)处连续。

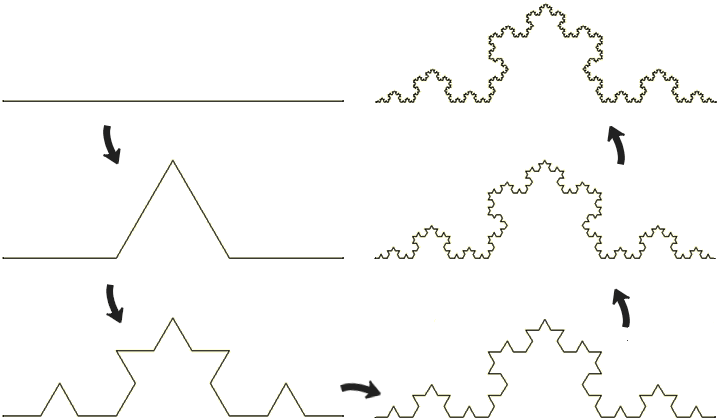
    回到我们的话题，如何构造一条曲线使得它可以填满整个平面。在这里我们仅仅说明存在一条填满单位正方形的曲线就够了，因为将此单位正方形平铺在平面上就可以得到填满整个平面的曲线。大多数人可能会想到下面这种构造方法：先画一条单位长的曲线，然后把它变成一个几字形，接着把每一条水平的小横线段变成一个几字形，然后不断迭代下去，最后得到的图形一定可以填满整个单位正方形。我们甚至可以递归地定义出一个描述此图形的函数：将定义域平均分成五份，第二和第四份对应两条竖直线段上的点，并继续对剩下的三个区间重复进行这种操作。这个函数虽然分布得有些“不均匀”，但它确实是一个合法的函数。最后的图形显然可以填充一个正方形，但它是不是一条曲线我们还不知道呢。稍作分析你会发现这条“曲线”根本不符合前面所说的ε-δ定义，考虑任何一个可以无限细分的地方（比如x=1/2处），只要ε<1/2，δ再小其范围内也有一条竖线捅破ε的界线。这就好像当n趋于无穷时sin(nx)根本不是一条确定的曲线一样，因为某个特定的函数值根本不能汇聚到一点。考虑到这一点，我们能想到的很多可以填满平面的“曲线”都不是真正意义上的连续曲线。为了避免这样的情况出现，这条曲线必须“先把自己周围填满再延伸出去”，而填满自己周围前又必须先填满“更小规模的周围”。这让我们联想到分形图形。

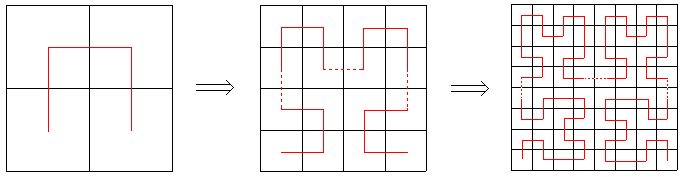
    德国数学家David Hilbert发现了这样一种可以填满整个单位正方形的分形曲线，他称它为Hilbert曲线。我们来看一看这条曲线是怎么构造出来的。首先，我们把一个正方形分割为4个小正方形，然后从左下角的那个小正方形开始，画一条线经过所有小正方形，最后到达右下角。现在，我们把这个正方形分成16个小正方形，目标同样是从左下角出发遍历所有的格子最后到达右下角。而在这之前我们已经得到了一个2×2方格的遍历方法，我们正好可以用它。把两个2×2的格子原封不动地放在上面两排，右旋90度放在左下，左旋90度放在右下，然后再补三条线段把它们连起来。现在我们得到了一种从左下到右下遍历4×4方格的方法，而这又可以用于更大规模的图形中。用刚才的方法把四个4×4的方格放到8×8的方格中，我们就得到了一条经过所有64个小方格的曲线。不断地这样做下去，无限多次地迭代后，每个方格都变得无穷小，最后的图形显然经过了方格上所有的点，它就是我们所说的Hilbert曲线。下图是一个迭代了n多次后的图形，大致上反映出Hilbert曲线的样子。
        

    根据上面这种方法，我们可以构造出函数f(t)使它能映射到单位正方形中的所有点。Hilbert曲线首先经过单位正方形左下1/4的所有点，然后顺势北上，东征到右上角，最后到达东南方的1/4正方形，其中的每一个阶段都是一个边长缩小了一半的“小Hilbert曲线”。函数f(t)也如此定义：[0,1/4]对应左下角的小正方形中所有的点，[1/4,1/2]就对应左上角，依此类推。每个区间继续划分为四份，依次对应面积为1/16的正方形，并无限制地这么细分下去。注意这里的定义域划分都是闭区间的形式，这并不会发生冲突，因为所有m/4^n处的点都是两个小Hilbert曲线的“交接处”。比如那个f(1/4)点就是左上左下两块1/4正方形共有的，即单位正方形正左边的那一点。这个函数是一条根正苗红的连续曲线，完全符合ε-δ定义，因为f(t-δ)和f(t+δ)显然都在f(t)的周围。
    Hilbert曲线是一条经典的分形曲线。它违背了很多常理。比如，把Hilbert曲线平铺在整个平面上，它就成了一条填满整个平面的曲线。两条Hilbert曲线对接可以形成一个封闭曲线，而这个封闭曲线竟然没有内部空间。回想我们上次介绍的Hausdorff维度，你会发现这条曲线是二维的，因为它包含自身4份，每一份的一维大小都是原来的一半，因此维度等于log(4)/log(2)。这再一次说明了它可以填满整个平面。

    Hilbert曲线的价值在于建立一维空间与二维空间一一对应的关系。Hilbert曲线可以看作是一个一维空间到二维空间的映射，也就是说我们证明了直线上的点和平面上的点一样多（集合的势相同）。Hilbert曲线也是一种遍历二维格点的方法，它同样可以用来证明自然数和有理数一样多。如果你已经知道此结论的Cantor证明，你会立刻明白Hilbert遍历法的证明，这里就不再多说了。当然，Hilbert曲线也可以扩展到三维空间，甚至更高维的空间，从而建立一维到任意多维的映射关系。下图就是一个三维Hilbert曲线（在迭代

    很多东西都是吹神了的，其中麦田圈之谜相当引人注目。上个世纪里人们时不时能听见某个农民早晨醒了到麦田地一看立马吓得屁滚尿流的故事。上面这幅图就是97年在英国Silbury山上发现的麦田圈，看上去大致上是一个雪花形状。你或许会觉得这个图形很好看。看了下面的文字后，你会发现这个图形远远不是“好看”可以概括的，它的背后还有很多东西。

    在说明什么是分形艺术前，我们先按照下面的方法构造一个图形。看下图，首先画一个线段，然后把它平分成三段，去掉中间那一段并用两条等长的线段代替。这样，原来的一条线段就变成了四条小的线段。用相同的方法把每一条小的线段的中间三分之一替换为等边三角形的两边，得到了16条更小的线段。然后继续对16条线段进行相同的操作，并无限地迭代下去。下图是这个图形前五次迭代的过程，可以看到这样的分辨率下已经不能显示出第五次迭代后图形的所有细节了。这样的图形可以用Logo语言很轻松地画出来。

    你可能注意到一个有趣的事实：整个线条的长度每一次都变成了原来的4/3。如果最初的线段长为一个单位，那么第一次操作后总长度变成了4/3，第二次操作后总长增加到16/9，第n次操作后长度为(4/3)^n。毫无疑问，操作无限进行下去，这条曲线将达到无限长。难以置信的是这条无限长的曲线却“始终只有那么大”。

        
    当把三条这样的曲线头尾相接组成一个封闭图形时，有趣的事情发生了。这个雪花一样的图形有着无限长的边界，但是它的总面积却是有限的。换句话说，无限长的曲线围住了一块有限的面积。有人可能会问为什么面积是有限的。虽然从上面的图上看结论很显然，但这里我们还是要给出一个简单的证明。三条曲线中每一条的第n次迭代前有4^(n-1)个长为(1/3)^(n-1)的线段，迭代后多出的面积为4^(n-1)个边长为(1/3)^n的等边三角形。把4^(n-1)扩大到4^n，再把所有边长为(1/3)^n的等边三角形扩大为同样边长的正方形，总面积仍是有限的，因为无穷级数Σ4^n/9^n显然收敛。这个神奇的雪花图形叫做Koch雪花，其中那条无限长的曲线就叫做Koch曲线。他是由瑞典数学家Helge von Koch最先提出来的。本文最开头提到的麦田圈图形显然是想描绘Koch雪花。

    分形这一课题提出的时间比较晚。Koch曲线于1904年提出，是最早提出的分形图形之一。我们仔细观察一下这条特别的曲线。它有一个很强的特点：你可以把它分成若干部分，每一个部分都和原来一样（只是大小不同）。这样的图形叫做“自相似”图形(self-similar)，它是分形图形(fractal)最主要的特征。自相似往往都和递归、无穷之类的东西联系在一起。比如，自相似图形往往是用递归法构造出来的，可以无限地分解下去。一条Koch曲线中包含有无数大小不同的Koch曲线。你可以对这条曲线的尖端部分不断放大，但你所看到的始终和最开始一样。它的复杂性不随尺度减小而消失。另外值得一提的是，这条曲线是一条连续的，但处处不光滑（不可微）的曲线。曲线上的任何一个点都是尖点。

    分形图形有一种特殊的计算维度的方法。我们可以看到，在有限空间内就可以达到无限长的分形曲线似乎已经超越了一维的境界，但说它是二维图形又还不够。Hausdorff维度就是专门用来对付这种分形图形的。简单地说，Hausdorff维度描述分形图形中整个图形的大小与一维大小的关系。比如，正方形是一个分形图形，因为它可以分成四个一模一样的小正方形，每一个小正方形的边长都是原来的1/2。当然，你也可以把正方形分成9个边长为1/3的小正方形。事实上，一个正方形可以分割为a^2个边长为1/a的小正方形。那个指数2就是正方形的维度。矩形、三角形都是一样，给你a^2个同样的形状才能拼成一个边长为a倍的相似形，因此它们都是二维的。我们把这里的“边长”理解为一维上的长度，那个1/a则是两个相似形的相似比。如果一个自相似形包含自身N份，每一份的一维大小都是原来的1/s，则这个相似形的Hausdorff维度为log(N)/log(s)。一个立方体可以分成8份，每一份的一维长度都是原来的一半，因此立方体的维度为log(8)/log(2)=3。同样地，一个Koch曲线包含四个小Koch曲线，大小两个Koch曲线的相似比为1/3，因此Koch曲线的Hausdorff维度为log(4)/log(3)。它约等于1.26，是一个介于1和2之间的实数。

    我们常说分形图形是一门艺术。把不同大小的Koch雪花拼接起来可以得到很多美丽的图形。如果有MM看了前面的文字一句也不懂，下面这些图片或许会让你眼前一亮。

放图前留下一句话：
Matrix67原创
转贴请注明出处

    原来我经常在想，要是有软件能帮我把图论题的数据画出来就好了。后来我想到一个制作这种软件的方法，就是把所有的点的位置设定为圆周上的等分点，这样可以最大限度的保证图象不致于太乱。我没想到居然有程序可以智能地决定哪个点、哪条边放在哪里更好看。
    我在OIBH的这个帖子里找到了这个好东西，它可以帮助OIer将大规模的图论题数据转化为图便于观察。今天我又用到了几次，突然想到把它介绍在我的Blog上。
    graphviz的主页设在http://www.graphviz.org，你可以在这里下载到最新的Windows版本，目前最新版本的安装程序为graphviz-2.12.exe。安装后你可以在dos下（任何目录中）调用它的命令行模式。
    这里，我们使用dot语言。官方网站上有关于dot语言的详细的用户手册，这里我只把常用的一些功能做一下演示。你可以在这篇日志的三个截图中掌握足够的知识来应用graphviz。
    先说明一下最顶上的Hello World程序。dot是程序名，参数-Tgif表示以gif格式输出，参数-O表示输出文件的方式设为默认（在当前目录下输出名为noname的文件，其后缀名与参数-T???所设定的类型相同）。下面一行输入的是graphviz所用的dot语言，digraph G表示有向图，花括号里描述图的内容。这样就生成了一个最简单的图。

    下面一个例子说明了如何输出一个边上有权值的无向图。这是OIer经常要用的东西。size=4,4指定了图的大小，单位为英寸。如果没有这一句的话，默认的图要大得多。你可以另外写一个程序把你的数据按图中的格式转化为dot代码。虽然graphviz可以从外部文件中读入这段代码，但我觉得粘贴进dos窗口更方便一些。

    下面这个例子包含更多的参数，展示了graphviz更多的功能。输出为ps文件更好看一些，因为输出ps文件可以反锯齿（应该是矢量的）。

    康托集合是闭区间[0,1]的子集，它的定义如下：给定区间[0,1]，把这个区间分成三段，去掉中间那一端（即去掉(1/3,2/3)），然后把剩下的两段中每一段都按照刚才的方法再进行操作，然后再分，再分，就这样一直挖洞挖下去。在第二次操作后，剩下的区间是[0,1/9]∪[2/9,1/3]∪[2/3,7/9]∪[8/9,1]，再操作一次后区间将由8段构成。最后剩下来的东西是什么呢？你能找到存在于这个集合中的某个具体的元素吗（不包括形如x/(3^n)的端点）？
    我们看到，n次操作后，区间的总长度为(2/3)^n，当n趋于无穷时，区间长度趋于0。但是这并不能说明这个区间里没有任何元素。事实上，我们可以找到至少一个元素。比如，下图中绿色的点表示三等分点，如果P满足AP/AB=A'P/A'B'的话，那么P点始终以比例相同的位置留在某一段上，这样的话即使无限地分下去也不会把它挖掉。
      
    P点的坐标可以通过解这个方程得到：x/1=(x-2/9)/(1/9)。解出来x为1/4。因此，1/4属于康托集合。当然，除了1/4之外还有很多点在这个集合内，我们只是找到了其中一个。事实上，康托集合内的元素有无穷多个。假如我们把所有0到1的数用三进制表示，那么我们发现，去掉的部分都是三进制小数里有数字“1”的。比如，第一次操作时，1/3和2/3的三进制分别是0.1和0.2，我们去掉的是所有从0.1到0.2的数（不包含端点，因为0.1也可以写成0.0222222222…）。第二次操作就去掉了百分位有1的那些数，依此类推。因此，只要一个位于0和1之间的三进制小数能够只用0和2写出，那么它就属于康托集合，因为它永远不会被去掉。刚才的1/4转化为三进制是0.020202…，因此它属于这个集合。显然，这样的数有无穷多个，比如三进制0.002002002…等于十进制的1/13，因此它也属于康托集合。同样，康托集合里不存在孤点，因为在它的左右可以找出无数个属于康托集合的数。应用对角线方法，这个集合里的元素居然还是不可数的。事实上，我们可以建立康托集合与闭区间[0,1]的一一对应关系。
    用以下方法可以把康托集合里的所有数与[0,1]的所有实数对应起来：将康托集合内的任意一个转化为三进制小数后，把每一个数字除以2，再当成是二进制小数转化回来。由于这些三进制小数里只含0和2，因此康托集合里的每个数都恰好能转化为一个[0,1]之间的二进制小数；同样地，二进制小数里的每个“1”变成“2”后也能得到一个康托集合里的数。
      
    设f为定义域在康托集合内的函数，定义f(x)为按照上面的转化方法x所对应的二进制小数，显然这个函数的值域就是[0,1]。比如1/3的三进制为0.0222…，而二进制0.01111…=0.1即十进制的1/2，因此f(1/3)=1/2。我们发现，2/3的三进制为0.2，而0.1的十进制也是1/2。于是f(1/3)=f(2/3)。类似地，那些被挖去的区间的两个端点对应的函数值都相同。现在，我们把这个函数的定义域也扩展到[0,1]：让康托集合里的那些被挖去的区间里的点的函数值与该区间对应的端点相同（在函数图象上看相当于把函数值相等的点用横线段连起来）。于是，f(1/2)=f(1/3)=f(2/3)=1/2，f(1/8)=f(1/9)=f(2/9)=1/4。这个函数一定是上升函数，它在长度为1的区间里从0增长到了1。同时，这个函数也是一个连续函数，因为康托集合与[0,1]的所有实数一一对应。这个函数是一个阶梯状的函数，但是它不是分段的，是连续的。它是无穷多个横线段组成的一个连续函数，除端点无意义以外导数值都是0。或者说，这个函数在不变之中上升。

做人要厚道
转贴请注明出处