Ambigram
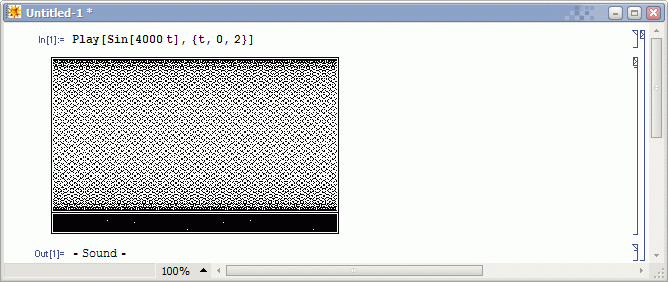
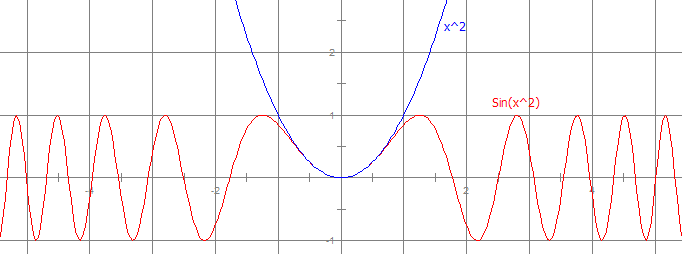
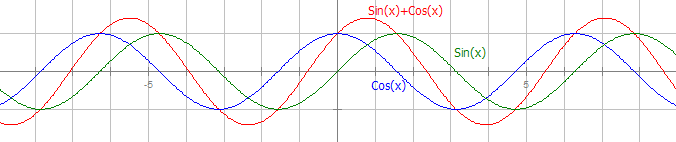
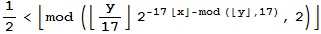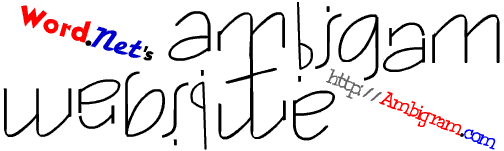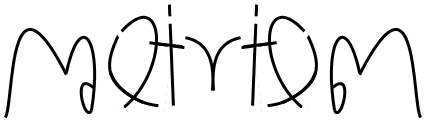Ambigram是指把一个单词或短语写成对称的样子，这样从两个不同的角度看这个图形都能读出这个单词或短语。例如，下面一个图形就是单词Ambigram的Ambigram：
ambigram.com的首页有个这样的图片：
Wikipedia上有这样一个Ambigram：
最后来看一个左右轴对称的Ambigram（献丑了）：
Erich Friedman教授为他的朋友创作了很多Ambigram。你可以在他的个人主页上看到。
Alphametic
Alphametic是指，把一句话写成加法算式，每一个字母表示一个数字，那么这个“虫食算”有唯一解。最常见的Alphametic可能是这个：
SEND + MORE = MONEY
它的唯一解是9567 + 1085 = 10652
另一些Alphametic如下：
FIFTY + STATES = AMERICA
TERRIBLE + NUMBER = THIRTEEN
EARTH + AIR + FIRE + WATER = NATURE
SATURN + URANUS + NEPTUNE + PLUTO = PLANETS
1969年，有人发现了这样一个有趣的Alphametic：
THREE + THREE + TWO + TWO + ONE = ELEVEN
这样的Alphametic叫做Doubly-True Alphametic。可以证明上面这个Doubly-True Alphametic是合法的Alphametic中“最小的”一个。另外两个稍微大一点的Doubly-True Alphametic为：
SEVEN + SEVEN + SIX = TWENTY
EIGHT + EIGHT + TWO + ONE + ONE = TWENTY
Mnemonic
Mnemonic本意是可以帮助记忆的句子。例如，我原来记together这个单词就记作We want to get her。再比如，arithmetic可以记作A Rat In Tom's House Might Eat Tom's Ice Cream（每个单词的首字母）。当然，也有一些专门搞笑的Mnemonic，比如Microsoft = Most Intelligent Customers Realize Our Software Only Fools Them，而Macintosh = Most Applications Crash. If Not, The Operating System Hangs。
数学家George Pólya（就是Pólya置换定理的那个Pólya）曾说过一句经典的话：How I need a drink, alcoholic of course, after the heavy chapters involving quantum mechanics! 依次数出每个单词的字母个数，你会惊讶的发现它正好是圆周率的前15位。后来又有人在后面加上一句All of thy geometry, Herr Planck, is fairly hard，让圆周率长度增加到24位。另一些圆周率的Mnemonic如下：
Can I have a large container of orange juice?
May I have a white telephone, or pastel color?
How I wish I could calculate pi faster.
For a girl I loved contrived; by nature tough, her heart survived.
下面这首诗给出了圆周率的前740位。其中10个字母的单词表示一个数字0，字母数大于10的单词则表示两位数。
Poe, E.
Near a Raven
Midnights so dreary, tired and weary.
Silently pondering volumes extolling all by-now obsolete lore.
During my rather long nap – the weirdest tap!
An ominous vibrating sound disturbing my chamber's antedoor.
"This", I whispered quietly, "I ignore".
Perfectly, the intellect remembers: the ghostly fires, a glittering ember.
Inflamed by lightning's outbursts, windows cast penumbras upon this floor.
Sorrowful, as one mistreated, unhappy thoughts I heeded:
That inimitable lesson in elegance – Lenore –
Is delighting, exciting…nevermore.
Ominously, curtains parted (my serenity outsmarted),
And fear overcame my being – the fear of "forevermore".
Fearful foreboding abided, selfish sentiment confided,
As I said, "Methinks mysterious traveler knocks afore.
A man is visiting, of age threescore."
Taking little time, briskly addressing something: "Sir," (robustly)
"Tell what source originates clamorous noise afore?
Disturbing sleep unkindly, is it you a-tapping, so slyly?
Why, devil incarnate!–" Here completely unveiled I my antedoor–
Just darkness, I ascertained – nothing more.
While surrounded by darkness then, I persevered to clearly comprehend.
I perceived the weirdest dream…of everlasting "nevermores".
Quite, quite, quick nocturnal doubts fled – such relief! – as my intellect said,
(Desiring, imagining still) that perchance the apparition was uttering a whispered "Lenore".
This only, as evermore.
Silently, I reinforced, remaining anxious, quite scared, afraid,
While intrusive tap did then come thrice – O, so stronger than sounded afore.
"Surely" (said silently) "it was the banging, clanging window lattice."
Glancing out, I quaked, upset by horrors hereinbefore,
Perceiving: a "nevermore".
Completely disturbed, I said, "Utter, please, what prevails ahead.
Repose, relief, cessation, or but more dreary 'nevermores'?"
The bird intruded thence – O, irritation ever since! –
Then sat on Pallas' pallid bust, watching me (I sat not, therefore),
And stated "nevermores".
Bemused by raven's dissonance, my soul exclaimed, "I seek intelligence;
Explain thy purpose, or soon cease intoning forlorn 'nevermores'!"
"Nevermores", winged corvus proclaimed – thusly was a raven named?
Actually maintain a surname, upon Pluvious seashore?
I heard an oppressive "nevermore".
My sentiments extremely pained, to perceive an utterance so plain,
Most interested, mystified, a meaning I hoped for.
"Surely," said the raven's watcher, "separate discourse is wiser.
Therefore, liberation I'll obtain, retreating heretofore –
Eliminating all the 'nevermores' ".
Still, the detestable raven just remained, unmoving, on sculptured bust.
Always saying "never" (by a red chamber's door).
A poor, tender heartache maven – a sorrowful bird – a raven!
O, I wished thoroughly, forthwith, that he&#
39;d fly heretofore.
Still sitting, he recited "nevermores".
The raven's dirge induced alarm – "nevermore" quite wearisome.
I meditated: "Might its utterances summarize of a calamity before?"
O, a sadness was manifest – a sorrowful cry of unrest;
"O," I thought sincerely, "it's a melancholy great – furthermore,
Removing doubt, this explains 'nevermores' ".
Seizing just that moment to sit – closely, carefully, advancing beside it,
Sinking down, intrigued, where velvet cushion lay afore.
A creature, midnight-black, watched there – it studied my soul, unawares.
Wherefore, explanations my insight entreated for.
Silently, I pondered the "nevermores".
"Disentangle, nefarious bird! Disengage – I am disturbed!"
Intently its eye burned, raising the cry within my core.
"That delectable Lenore – whose velvet pillow this was, heretofore,
Departed thence, unsettling my consciousness therefore.
She's returning – that maiden – aye, nevermore."
Since, to me, that thought was madness, I renounced continuing sadness.
Continuing on, I soundly, adamantly forswore:
"Wretch," (addressing blackbird only) "fly swiftly – emancipate me!"
"Respite, respite, detestable raven – and discharge me, I implore!"
A ghostly answer of: "nevermore".
" 'Tis a prophet? Wraith? Strange devil? or the ultimate evil?"
"Answer, tempter-sent creature!", I inquired, like before.
"Forlorn, though firmly undaunted, with 'nevermores' quite indoctrinated,
Is everything depressing, generating great sorrow evermore?
I am subdued!", I then swore.
In answer, the raven turned – relentless distress it spurned.
"Comfort, surcease, quiet, silence!" – pleaded I for.
"Will my (abusive raven!) sorrows persist unabated?
Nevermore Lenore respondeth?", adamantly I encored.
The appeal was ignored.
"O, satanic inferno's denizen — go!", I said boldly, standing then.
"Take henceforth loathsome "nevermores" – O, to an ugly Plutonian shore!
Let nary one expression, O bird, remain still here, replacing mirth.
Promptly leave and retreat!", I resolutely swore.
Blackbird's riposte: "nevermore".
So he sitteth, observing always, perching ominously on these doorways.
Squatting on the stony bust so untroubled, O therefore.
Suffering stark raven's conversings, so I am condemned, subserving,
To a nightmare cursed, containing miseries galore.
Thus henceforth, I'll rise (from a darkness, a grave) — nevermore!
— original: E. Poe
— Redone by measuring circles.
Lipogram
看看下面这句话有什么问题？
This is an unusual paragraph. I'm curious how quickly you can find out what is so unusual about it. It looks so plain you would think nothing was wrong with it! In fact, nothing is wrong with it! It is unusual though. Study it, and think about it, but you still may not find anything odd. But if you work at it a bit, you might find out! Try to do so without any coaching!
答案：这段话里竟然没有一个字母e ！
Lipogram就是指的这样一个段落（甚至文章），里面缺少某个常用的字母。在所有的Lipogram中，写一个没有字母e的文章是最难的，因为字母e出现的频率最高。
看一个比较长的Lipogram。下面这篇文章里硬是没有一个字母e！
Looking at this paragraph with confusion? I'll aid you slightly. Is any odd gap, lacuna or omission obvious to you? Got it now? No?
That's right – this is a lipogram – a book, paragraph or similar thing in writing that lacks a symbol, particularly (but not always) that symbol fifth in rank out of our 26 script-signs (found amidst 'd' and 'f'), which stands for a sound such as that in 'kiwi'. I won't bring it up right now, to avoid spoiling it. I could play with lipograms morning, noon and night. So it is with joy that I submit to you this location – truly, a loquacious location – for lipogram fanatics to join as a unit to glorify this form of wordplay.
As far as I know, this location has a distinct honour: it contains such an abundant quantity of words without using this taboo glyph that no WWW location can outmatch it. As of right now, it contains 1500 words without any hint of that symbol. Naturally, many long lipograms abound in print, including books, rhyming stanzas, and similar works of fiction. Most notably, La Disparition (A Void) by a famous author of a writing group known as Oulipo, stands out as a paragon of lipogrammaticity. I cannot aim to surpass it, but as a fan, I can look upon it with admiration.
Writing lipograms is, as you might think, a difficult task. In my lingo, 2/3 of all words contain that symbol which I am now avoiding, including many common pronouns and similar words commonly found in writing. Without using abbrvs., slang and odd jargon, which most purists scorn as cop-outs, it's darn tough to impart information in a stylistically satisfying way. Stripping paragraphs of particular symbols has a way of making looking at lipograms jarring. No doubt about it, a lipogram is a particularly arduous form of wordplay.
Having said this, acquiring a knack for lipogram composition isn't that hard, and may assist you in your non-lipogrammatic writing. Not to say that I'm without aid in this activity; my dictionary is always handy, as is a book with synonyms for words. And, notwithstanding any drawbacks flowing from passing many an hour looking for unusual ways to say ordinary things, it might aid your socialization skills. Chicks truly dig lipogrammatists, or so my old lady says.
Sadly, a handful of critics find lipograms ridiculous, ugly or without worth (as fiction or as wordplay). To such sorry saps, I say only that in constraining your thoughts and writing in a particular way aids in promoting branching paths of thought, thus amplifying vocabulary and instilling adroit linguistic skills among both young and old. By putting into praxis ways of thinking that wouldn't occur normally, lipograms call for authors to look at writing as an activity in ways that, frankly, wouldn't occur to such niggling adjudicators of linguistic conduct.
Withholding a symbol found in so many words has drastic symptoms that disallow many topics of discussion. (From this point on, I'll stick to talking about that sign I'm skipping right now). Using math is almost an impossibility; you can only main
tain 15 of all non-digital words for cardinal quantity up to 100, and hardly any at all past that point, though using digits is a good way out. You can go north or south, but talking about circumnavigating our world latitudinally is an impossibility. How can I possibly talk about various kinds of malt liquor, or parts of my body, without it? To top it all off, as an Anglo, strict prohibitions apply to naming of my own form of linguistic communication. I ought to thank my lucky stars that I'm not writing in lipogrammatic français, though, which holds on to only an octal portion of its original vocabulary.
But all is not lost. Surprisingly, profanity is mostly intact. As a practicing lipogrammatist, you'll find you want many such words, for it is a task so awkward as to call for cussing and cursing on a normal basis. A world map is truly a blissful oasis; my country (Canada) is totally satisfactory, as with most toponyms for nations (111 out of 186, by my count); with a bit of work, USA, UK, and so on, can still show up, and with twin island nations Trinidad and Tobago and Antigua and Barbuda (both with 17 glyphs) topping my list for prolongation. Musicians (particularly classical artists), astonishingly, hold firm as topics of discussion, with Bach, Bartok, Brahms, Chopin, Dvorak, Haydn, Holst, Liszt, Mozart, orff, Puccini, Rachmaninov, Rossini, Scarlatti, Schumann, Strauss, Stravinsky, Tchaikovsky and Vivaldi void of my lost non-consonant.
An additional branch of family Lipogrammatica consists of univocalics. This form of wordplay is akin to a lipogram, but contains a solitary sign that's not a consonant. To wit, a univocalic might omit 'a', 'i', 'o', and 'u' (but what about 'y'?). A univocalic has a sonorant quality that a lipogram lacks, so you must look at a lipogram, but contrarily, a univocalic is both auditory and visual, and has a strong sound if said aloud. Univocalic writing is hard to pull off, but if it's good, its payoff is gigantic.
另外推荐本Blog里的两个相关内容：
http://www.matrix67.com/blog/article.asp?id=104
http://www.matrix67.com/blog/article.asp?id=173
Matrix67收集整理
转贴请注明出处
