你认为是否有可能存在这样一个函数f：在平面上随便画一个圆，圆里面总能够找到函数图像上的一个点？继续看下去前，不妨先仔细思考一下。
为了说明任一圆内都包含函数上的点，我们只需要说明对于平面上任意给定点(x,y)，对于任意小的d都能在函数上找到一点，使得其横坐标落在x±d的范围内且纵坐标落在y±d内。这样的话，任意给出一个圆后，我都能保证圆的内接正方形里有点。
我们构造这个函数f的基本思路是，构造一个将全体有理数映射到全体有理数的函数。注意到有理数是可数的，我们可以用这里的方法将全体有理数和自然数建立一一对应关系。也就是说，我们有了一个定义域为全体自然数、值域为全体有理数的一对一函数R(x)，它所对应的函数值是第x个有理数。下面我们开始着手定义我们要求的函数f(x)。函数f(x)的定义域是全体有理数，定义域里的每个x都可以表示成n/m的形式（化到最简），于是我们可以令f(x)=f(n/m)=R(m)。对于任意的y和d，在y±d里肯定存在一个有理数，假如按照上面的对应来看它是第m个有理数（即R(m)），下面我们就想办法说明我们总能够找到一个n，使得n/m在x±d的范围内。当然，如果运气不好m值很小的话我们就挂了，我们很自然地想到，这个m值应该越大越好，最好能重新定义一个值域为全体有理数的函数，对任一给定的有理数我们都能找出任意大的m对应到它。然后我们想到定义一个多对一的、定义域和值域都是自然数的函数H(x)：
x 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 …
H(x) 1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 …
重新定义f(x)=f(n/m)=R(H(m))，这样的话任意给定一个有理数，我们可以找到任意大的m使得R(H(m))等于这个有理数。当m足够大时，m(x-d)和m(x+d)之间一定会出现一个整数n，则此时n/m在x±d的范围内。
但我们又遇到一个问题：要是找到的那个n始终不能和m互质（表明没化到最简）咋办？我的直觉是，这种极端的情况应该是不存在的，当m充分大时，总有一个满足要求的n/m出现。但我没有严格证明它。其实，我根本不需要去证明它；这个题目有趣就有趣在，我这个函数f是可以随便构造的。你或许在想，要是分母m为质数就好了。那好，我就可以强迫分母m为质数。定义一个定义域为全体质数，值域为全体正整数的函数P(x)，它表示x是第几个质数：
x 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 …
P(x) – 1 2 – 3 – 4 – – – 5 – 6 – – …
重新定义f(x)=f(n/m)=R(H(P(m)))，现在我们能够找到任意大的质数m使得R(H(P(m)))等于指定的有理数。当m足够大时，m(x-d)和m(x+d)之间一定会出现两个相邻的整数p和q，由于m是质数，p和q之间总有一个数与m互质（不可能都是m的整倍数），我们需要的n也就找到了。
满足要求的函数有很多。这只是其中一种构造方法。大家能不能再想一些更有趣的构造来？
来源：http://www.douban.com/group/topic/2561708/
参考网友yushih的解答
最近重新整理了日志Tag。如果你喜欢这篇文章，不要错过这里的惊奇数学事实，你会看到更多难以置信的数学结论。
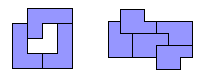由单位正方形拼接而成的图形叫做多联骨牌(Polyomino)。一个有趣的问题是，能否用奇数个相同的多联骨牌拼成一个对称图形？答案是肯定的。右图显示了如何用奇数个相同的多联骨牌拼接出中心对称图形和沿对角线方向轴对称的图形。
