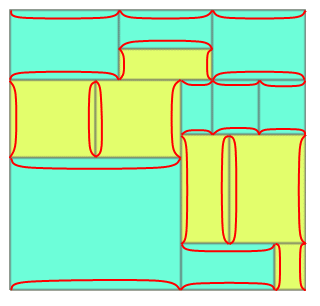
接下来,我们用图论方法来证明:一个由小矩形拼接而成的大矩形,若每个小矩形都有至少一条整数长的边,则大矩形也有至少一条整数长的边。考虑图中每个矩形的每个顶点,把它们作为图G的顶点集(相邻矩形重合的顶点并作一个点);对于每一个小矩形,把它整数边方向的两对顶点分别用一条边连接起来(相邻矩形公共边上的重边不合并)。如果哪个小矩形四条边都是整数,无妨随意把它当作横向整数边的或者纵向整数边的,连接任一种方向上的边。这样的话,每个矩形恰好产生两条边。注意这个图的一些很显然的性质:度为1的点只有4个(大矩形的四个角),其余的顶点的度都是偶数(只能是2或者4)。下面,我们把这个矩形放在平面坐标系上,大矩形的左下角对齐原点(0,0)。从原点开始沿着图G的边走(每条边最多走一次,不走走过的边),显然走到的每个点都满足这个性质:它的两个坐标均为整数。但我们的出发点是一个度为1的点,在走到另一个度为1的点之前,我们遇到的所有顶点的度都是偶数。因此只要没走到另一个度为1的点,我们就不可能走死。但是,图G总的边数有限,总有一个时候我们将不能再走。因此,这次旅程的终点必然落在另一个度为1的点上。这个终点是大矩形的另一个角,它的两个坐标值均为整数。命题得证。
图形
经典证明:Cantor-Bernstein-Schroeder定理
明天考英语,单词还没背。先冒死更新一个^_^
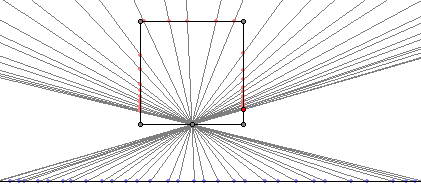
我们称一个从集合A到集合B的映射是“单射”的,如果A中的任两个相异元素都不会映射到B里的同一个元素。如果一个A→B的映射是单射的,并且B里的所有元素都被射了(满射),那么这个映射就是“双射”的。Cantor-Bernstein-Schroeder定理是说,假如存在一个从集合A到集合B的单射函数f,以及一个从集合B到集合A的单射函数g,那么A与B之间一定存在一个双射函数(即能建立起一一对应的关系,两个集合有相等的势)。这个结论并不是显然的。对于无穷集合,我们可以构造出很多这样的例子,两个映射A→B和B→A都是单射,但都不是满射的。例如,给定一个正方形和正方形外的一条直线,把正方形放到直线上滚一圈所形成的对应关系是一个从正方形上的所有点到直线上的点的一个单射函数,而连接直线上的点和正方形一边中点后与正方形的另一个交点构成了一个从直线到正方形的单射关系(如图)。那么,根据Cantor-Bernstein-Schroeder定理,我们一定可以找到一种函数,使得直线上的所有点和正方形上的所有点有一一对应的关系。
Ubigraph:强大而易用的图论动画生成软件
Ubigraph是一个全新的图论动画生成软件,利用它你可以快速生成图论模型的图形和动画,直观地展示出各种图论模型的三维结构,演示各种图论算法的过程,非常适合用于研究和教学。之前本Blog曾经介绍过一个类似的软件graphviz,但这里提到的Ubigraph显然更强大一些。上面的动画就是由Ubigraph生成的二叉查找树演示动画(高清版here),看上去相当的酷。值得一提的是,Ubigraph也是相当易用的。graphviz有它自己的语法规则,而Ubigraph则直接支持Python, Ruby, PHP, Java, C, C++等几乎所有主流语言,因此不管你原先使用的是什么语言,你都可以很快地融入到Ubigraph来。例如,在C语言中包含一个头文件UbigraphAPI.h,你便可以像往常一样用循环语句“画”一个环。
#include <UbigraphAPI.h>
int main(int const argc, const char ** const argv)
{
int i;
for (i=0; i < 10; ++i)
ubigraph_new_vertex_w_id(i);
for (i=0; i < 10; ++i)
ubigraph_new_edge(i, (i+1)%10);
sleep(2);
ubigraph_clear();
}
你可以在这里下载这个软件。目前该软件暂时没有Windows版。
趣题:在指定形状的棋盘内放置n个相同的图形
上个月Erich Friedman的Math Magic提出了这样的问题:
给定一个指定形状的棋盘,给定一个大于2的整数n,找出一个面积最大的图形S使得n个S能够不重叠地装进这个棋盘里。
问题提出之后得到了不少有趣的构造,这些构造是否为最优解还有待进一步证明。
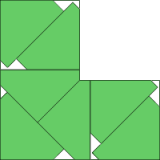
由三个格子组成的棋盘共有两种本质不同的形状。“长条形”已经不用多考虑,“拐角形”中n=2, 3, 6时的最优解也是非常显然的。拐角形棋盘是可以分成四等分的。但是,在这个棋盘中放置5个相同的图形就没那么容易了。已知的最优方案占据了整个棋盘约0.959的面积。放置7个相同的图形研究起来更困难一些。已知最优解为0.956。


代数曲面画廊
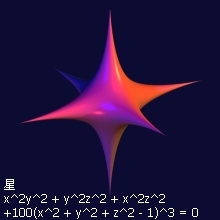







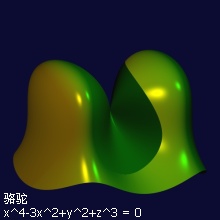



查看更多:http://www1-c703.uibk.ac.at/mathematik/project/bildergalerie/gallery.html
(德语,Stetson MM快来翻译)