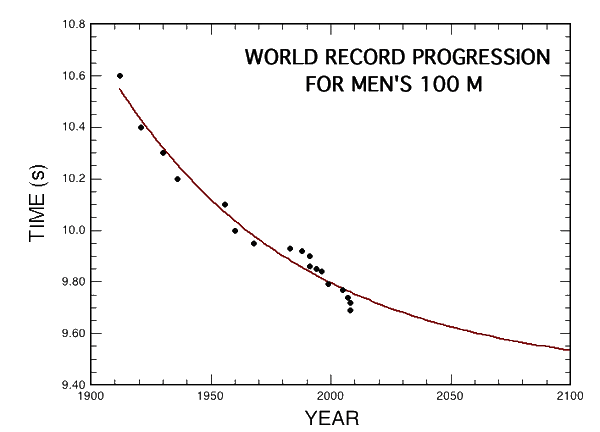
看来，已经有人提前做了一件我最近一直想要做的事情。
最近的几个有点不正常的数据点估计把整条曲线拉低了不少。
来源：http://blog.wired.com/wiredscience/2008/08/bolt-is-freaky.html
图形
双向Josephus问题中的分形图形
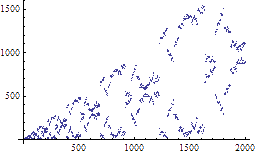Daisuke Minematsu和他的同学们发现，Josephus问题中也隐藏着分形图形。Josephus问题是初学编程的人必然会接触到的一个问题——n个人围成一圈进行1到k报数，每次报到k的人退出游戏（离开这个圆圈），那么最后剩下的那个人是谁。在这里，我们考虑一个Josephus问题的变种：双向Josephus问题。双向Josephus问题中有两个交替进行的报数进程，其中一个按顺时针方向踢出每第k个人，另一个进程则逆时针踢出每第k个人。两个进程交替进行，直到最后只剩一人为止。假如n=10, k=3的话，第一个退出的人是#3，第二个退出的人是#8，第三个退出的人是#6，以后分别是4, 10, 9, 5, 1, 7，最后剩下的人是2。我们用S(n,k)来表示在相应的n值和k值的情况下最后剩下的那个人的编号，对于每个固定的k值，函数S的图象竟然都是一个分形图形。右图是S(n,4)所对应的图象，你可以非常清楚地看到这个图象的自相似性。你可以自己用Mathematica来验证一下。
趣题：最小的可覆盖所有12种五联骨牌的图形
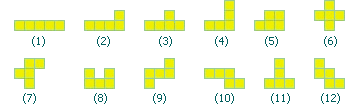
IBM Ponder This上个月的题目：一个多联骨牌(polyomino)是指平面上若干个正方形相接拼成的图形。经过旋转、镜像得到的图形仍然视为相同的多联骨牌。如上图所示，五联骨牌一共有12种。我们说一个多联骨牌A覆盖B，如果我们能在B上添加若干个新的方块得到A。回答下面两个问题：
1. 一个六联骨牌最多可以覆盖多少种不同的五联骨牌？
2. 给出一个最小的能够覆盖所有12种五联骨牌的图形。
O3 ·7 ·5 ·5 ·4 ·7 ·6 ·6 ·7 ·?
在ahapuzzles.com逛了一天，看到了不少好玩的东西。
Update: 刚收到Lloyd King发来的邮件，我很高兴。所有这些谜题都是他创作的。他有一本书就叫做Amazing “Aha!” Puzzles，里面全是让人拍案叫绝的谜题。
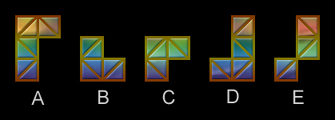
问号处应该填哪一个图形？
答案：E。各方块的对角线组成了数字3、4、5、6、7的字样。
问号处应该填什么数字？
答案：5。圆圈和点表示太阳和9大行星，旁边的数字表示每颗星球的名字的字母个数。
一个与矩形剖分有关的命题（三）：诡异的微积分证明
如果一个矩形可以分割为若干个小矩形，每个小矩形都有至少一边为整数长，则原矩形同样有至少一个长度为整数的边。换句话说，用至少有一边的长度是整数的小矩形拼成一个大矩形，大矩形也有至少一条整数长的边。
在这个命题的所有常见的证明方法中，我总觉得这个证明是最诡异的。真不知道第一个想出这个证明方法的人是怎么思考出来的。把矩形放在平面直角坐标系上，左下角对齐原点(0,0)。考虑函数e^(2 · pi · i · (x+y))在每个小矩形上的积分（展开并分离变量分别积分）：
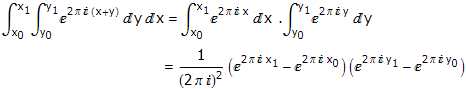
显然，这个式子等于0当且仅当(x1-x0)和(y1-y0)中至少一个是整数（也即至少有一边的长度是整数）。考虑函数在整个大矩形上的积分，它可以拆成各个小矩形上的积分的和，因此结果仍然是0。这说明，大矩形至少有一条整数长的边。