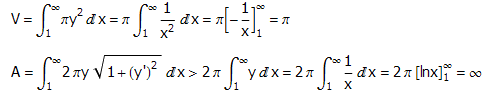打完了World of Goo，确实是一个难得一见的好游戏。自从打完Portal后，很久没玩到这么好的游戏了。遗憾的是呢，和Portal一样，这个游戏的关卡并不难，游戏时间也太短了一些。一款好的游戏会设置一些在游戏通关后仍然具有可玩性和挑战性的环节，比如这个游戏中你的终极目标就是反复挑战关卡收集尽可能多的球球，在Tower of Goo里面建造尽可能高的塔。如何用尽可能少的球球来建造一个尽可能高的、稳定的塔呢？受到经典分形图形Sierpinski三角形的启发，我打算建这么一个塔（下图为草图），这个样子看上去蛮稳定的（大家认为呢？），并且节省了不少材料。由于球球是可以重新安放的，因此我可以在搭建好三角形后从中间挖出不要的球球来，这给我建造Sierpinski三角形提供了可能性。不过，目前这个工程只做到了2阶，因为我还差球球。大家还想到了什么其它的结构？欢迎在下面和大家分享。
有时候，一个看似更加复杂的问题反而有一个更简单的解答。
四色问题是说，对一个平面地图进行染色，要想用不同的颜色来区别相邻的区域，最少需要多少种颜色。在很长一段时间里，人们猜想，只要四种颜色就足够了；但这个“四色猜想”却怎么也证不出来。直到上世纪70年代，“四色猜想”才在计算机的帮助下获得证明。在《从一到无穷大》一书中，作者提到了这样一个有趣的事实：平面上的四色问题一直是一个相当复杂的难题，然而有意思的是，在环面上的染色问题却只需要短短十几行文字就能得出一个完美的结论。下面我们来说明，给一个游泳圈上任意划分出来的区域进行染色，为了使相邻区域不同色，只需要7种颜色就够了。
为了证明这一点，我们只需要说明，在一个环面图中总能找到一块区域，它的邻域不超过6块。如果真是这样的话，余下的部分用数学归纳法就直接证到了：对于一个有n个区域的图，我们找出它的一个邻域数量不超过6的区域，然后把这块区域缩小为一个点，使整个图的区域个数减少到n-1。按照我们的数学归纳，这个有n-1个区域的图是可以7染色的；并且显然地，把第n个区域添加回去后所产生的图仍然可以7染色，因为我的邻域不超过6个，我总能找一个和这些邻域都不一样的颜色。
现在的问题就是，为什么总存在邻域数量不超过6的区域呢？注意到在环面上，有V+F-E=0，其中V表示顶点数，F表示区域数，E表示边的总条数。注意到每个顶点都发射出了至少三条边，即所有顶点引出的边数至少为3V；但每条边都被重复计算了一次（因为一条边有两个端点），因此3V/2≤E，即3V≤2E。代入V+F-E=0，得到E≤3F。假设每个区域都有7个或7个以上的邻域，那么它们将产生至少7F条边；但每条边都被重复计算了一次（因为每条边都为两块区域共享），因此7F/2≤E，即7F≤2E。于是，2E≥7F>6F≥2E，矛盾。
看到新词就上一下Wikipedia确实是一个好习惯。前一篇日志的那个pdf里作者提到了Gedankenexperiment(Thought experiment)，上Wikipedia一查果然学到了牛B的新东西。好多物理定律其实完全是由思维实验推导出来的，难以置信仅仅是思考竟然就能得出物理世界遵从的各种法则。经典的物理思维实验有Newton大炮、Galileo斜塔实验、Schrödinger的猫猫、Maxwell的妖怪等等。还有，Turing机也是一个伟大的思维实验。
数学上的不少悖论（特别是涉及到维度和无穷的悖论）都是相当有趣的思维实验。Gabriel喇叭是y=1/x在[1,+∞)上的图象沿x轴旋转一周所形成的旋转体。这个简单的三维图形有一个奇特的性质：它的表面积无穷大，却只有有限的体积。为了证实这一点，只需注意到：
Gabriel喇叭会导出一个非常诡异的悖论：如果你想用涂料把Gabriel喇叭的表面刷一遍，你需要无穷多的涂料；然而把涂料倒进Gabriel喇叭填满整个内部空间，所需要的涂料反而是有限的。
有网友一定会问，那有没有什么二维图形，面积有限大，周长却无限长呢？答案是肯定的，Koch雪花就是这样一个经典的例子。不过，通过分形构造出来的这类图形似乎并不存在涂料悖论，因为递归到一定深度时分形图形的尺度将小于表面涂料的厚度，因此表面大小不能永无止境地算下去，涂满表面所需的涂料不再是无穷多。当考虑到涂料厚度时，原先的悖论也可以解释清楚了：填充内部空间仅仅涂满了图形的内表面，一旦考虑到涂料的厚度，它和外表面的区别就出来了。
如果一个矩形可以分割为若干个小矩形，每个小矩形都有至少一边为整数长，则原矩形同样有至少一个长度为整数的边。换句话说，用至少有一边的长度是整数的小矩形拼成一个大矩形，大矩形也有至少一条整数长的边。
我们首先把每个小矩形都分割成单位长或单位宽的长条。这样的话，大矩形里就只有两种小矩形：宽为1的（图(2)中的蓝色矩形）和高为1的（图(2)中的红色矩形）。我们对蓝色矩形的个数施归纳。随便选择一个蓝色的矩形（例如图(2)中的阴影矩形）。增加它的高度，让它“穿过”它头顶上的红色矩形（把它正上方的红色矩形截成左右两段），直到这根竖条状矩形的顶端碰到了另一个蓝色矩形的底端。把那个矩形作为新的操作对象，继续增加其高度（并可能再次更换“当前矩形”），直到达到整个大矩形的上边界。我们用同样的方法让最初所选的阴影矩形向下“生长”到大矩形的下边界。注意到在此过程中，蓝色矩形始终保持着单位宽度，红色矩形始终保持着单位高度。整个过程结束后，红色矩形变多了，但蓝色矩形的个数不变。此时我们得到了一条上下贯穿整个大矩形的蓝色矩形链。把它们擦掉，将右半部分左移一个单位，重新拼成一个大矩形。新的大矩形高度不变，宽度减一（因此原来的整数边还是整数，非整数边仍然不是整数），并且最关键的是蓝色矩形的个数减少了。反复进行这样的操作，总有一个时候大矩形里只剩下红色的矩形（则原大矩形高度显然为整），或者某次操作后所有矩形都被去掉了（则原大矩形宽度为整）。
借用这种方法我们还可以得到一个有点搞笑的反证法。假设大矩形的横边竖边都不是整数。每一步操作后，这两个边仍然是非整数，这表明大矩形里不可能只剩一种颜色的小矩形，于是我们可以无限制地调用上面的操作。最后的结果是：我们得到了一个用整数长或整数宽的小矩形拼接而成的一个横边竖边都小于1的大矩形！这显然是荒谬的。
参考资料：http://www.cut-the-knot.org/Curriculum/Algebra/IntRectRobinson.shtml
