上次说到维度时，有人提到了如何理解四维空间的问题。这是一个非常有趣的话题，可是我一直没有用心写一下。前段时间网上出了一部片子叫做Dimensions: a walk through mathematics，据称里面详细介绍了四维空间。我本以为推荐一下这个片子就能少写一篇又臭又长的日志了的，没想到下下来看了之后发现该片奇差，不了解四维空间的人看了半天估计还是不了解四维空间。最近放假比较闲，打算慢慢来扯一下。如果你以前从来没细想过四维空间的话，相信今天你会有一种超凡脱俗的感觉。
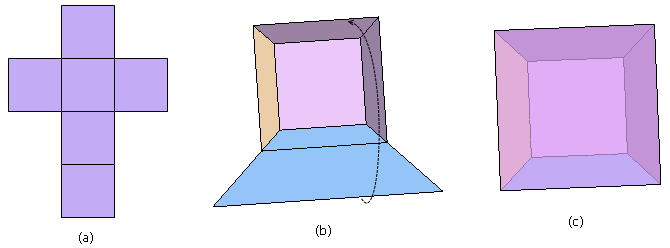
现在，假设我是一个二维世界的人，我不能理解什么是“高度”，什么是“体”，什么是“空间”。你想向我描述三维世界中的立方体。你该怎么说呢？你或许会从立方体的展开图开始谈起：图(a)就是一个立方体的展开图，如果我们剪一个这种形状的纸板，我们可以把它折成一个正方体。我开始好奇了。
这是一个由“L”形三联骨牌拼成的图形。你能看出这个图形有什么神奇的地方吗？
答案：每一个“L”形板块都与另外四个“L”相邻。这是目前已知的满足这种性质的最小构造。“中心对称”并不是我们想要的答案。我们能用“L”形骨牌轻易构造出大量满足中心对称的简单图形来。
由n个单位正方形拼接而成的图形叫做n联骨牌。一联骨牌和二联骨牌显然都只有一种。三联的有两种（长条形和拐角形）。四联、五联、六联和七联骨牌则分别有5种、12种、35种、108种。有牛人竟然把所有这些多联骨牌拼成了一个圆形，更神的是12个五联骨牌的位置让整个圆盘变成了一个钟表的盘面！这12个五联骨牌正好分布在圆盘周围12个间距相当的地方，其中5和10的位置分别用罗马数字V和X表示，9和12则用英文首字母N和T表示。圆盘中间是一联、二联、三联、四联骨牌，外围是35个六联骨牌，再外面则是107个七联骨牌。第108个七联骨牌——中间有一个空洞的特殊骨牌——则被放在了整个圆盘的正中间。
通过不断的杂交、变异并与原作比较确定适应度，经过904314代后，终于得到了一个满意的结果。
来源：http://rogeralsing.com/2008/12/07/genetic-programming-evolution-of-mona-lisa/
Update: 给一个JavaScript实现的地址，可在线测试 http://alteredqualia.com/visualization/evolve/
Escher在创作上面这幅画时曾经做了一张草图。受此启发，Steve Witham绘制了下面这张图纸。在这样的图纸上作图要有多牛B就有多牛B。假如以左下角的那个小圆点为(0,0)，曲线y=1走着走着就变成y=1/4了，而x=1则慢慢变为了x=4。
