阴阳图是由两个半圆弧相接组成的曲线把整个圆平分为黑白二色而成。1958年，英国数学家Henry Dudeney在他的著作Amusements in Mathematics中曾经提出了这样一个问题：如何用尺规作出一条同时平分阴阳两部分的曲线？他给出了两种不同的答案。
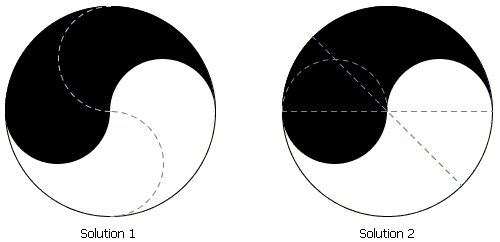
第一种方法是非常完美的，它不但同时平分了阴阳两部分的面积，连分出来的形状也完全相同。另一种办法也非常简单，仅用一条45度倾斜的直线即可同时平分阴阳两部分。为了证明这一点，我们只需要计算一下白色的半圆形和45度扇形的面积和即可。二者的面积恰好都等于πR^2/8，其总和为πR^2/4，恰为整个白色区域的一半。由对称性，黑色面积也被平分。除此之外，你还能想到多少种平分方法呢？
我们上次说到，不是所有的平面图都是可4选择的。于是人们接着猜想，是不是所有平面图都是可5选择的呢？1994年，Carsten Thomassen证明了，所有平面图都是可5选择的。这个证明极其简单，论文全文不足两页，证明过程仅十多行。证明对平面图中的区域数n施归纳。有趣的是，归纳的命题比我们待证明的命题要强得多，否则原命题反而证不到。
为简便起见，我们假设平面图是一般的，它没有同属于四块区域的交界点，也没有中空的“洞”。加入这些条件不会让问题变得更简单，因此这些假设都是合理的。下面再假设最外面那一圈区域（与“外部空间”相邻的区域）有s个，它们彼此相连构成了一个环，我们按逆时针顺序把它们分别记为P_1, P_2, P_3, …, P_s。无妨设P_1和P_2的颜色分别为1和2。下面我们证明一个比原命题更强的结论：若最外面那s个区域的颜色列表中至少有三个颜色，其余那些（被围在内部的）区域的颜色列表中有五个颜色，则一定存在合法的列表染色。当区域数n足够小时结论显然成立。
四色定理告诉我们，给地图上的每个区域涂一种颜色，为了使相邻的区域有不同的颜色，我们总共只需要4种颜色就够了。不过，万一有些省装怪，偏不喜欢分配给它的颜色该咋办？这下问题就变得有意思起来了。为了满足不同省市的要求，国家测绘局可以在为地图染色前先让每个省市列出自己能够接受的几种颜色，染色时就只从每个省市给出的候选颜色中取色。我们把每一个使得相邻区域的颜色互不相同的染色方案叫做一种列表染色(list coloring)。现在的问题是，至少要求每个省市列出多少个候选颜色才能使合法的列表染色总是存在，不管这些颜色列表是什么？如果每个省市列出k种颜色就足够了，我们就称该地图是可k选择的(k-choosable)。或许大家会想，k=4就够了吧，毕竟四色定理保证了只使用4种颜色一定能实现合法的染色，而在列表染色问题里总的颜色很可能还不止4种，同时相邻区域的公共颜色数量也将减少。但是，数学家们早就注意到，能够k着色的平面图不见得就一定可以k选择。例如，下面这个图显然可以二着色，但它就不是二选择的——如果每个区域的颜色列表如图中所示，则不存在满足要求的列表染色。因此，人们普遍认为，并不是每个平面图都是可4选择的。
不过，数学家们一直没能找到不可4选择的平面图。1993年，Voigt发现了第一个不能4选择的平面图，它有238块区域。构造方法非常具有启发性，从里面能看到不少数学思维方法。
昨天我突发奇想，写了几段Mathematica代码，生成了各种排序算法的内存变化图。图中每一个新的横行都表示数组的一次更新，数字大小用颜色来表示。你可以直观地看到这些算法是如何把乱序数组一点一点变为有序的。效果还是很令人满意的，不少算法的内存轨迹都相当美观，相当有艺术性。
图很大，我就不在首页上显示了，大家点“查看更多”看图吧。
我为最新一期的《博物》杂志写了一篇关于七巧板的文章。文章中我提到了一个有趣的问题：一副七巧板拼出的图形里最多可以有多少个中空的“洞”？Martin Gardner认为，一块副七巧板最多能拼出有三个洞的图形，并且他自己给出了一个非常漂亮的构造。如果你手中有七巧板的话，不妨也来试试看；没有七巧板也不必觉得遗憾，网上遍地都是七巧板Flash游戏。觉得困难的话，不妨先从两个洞开始做起。
注意，一个中空的洞必须完全被七巧板的内部空间所包围，仅仅是端点相触由七巧板边界围成的洞是不算的。因此下面的图形中其实只有一个洞，另外两个都不符合规范。
