下面这个有趣的问题来自IMO 2008第一题，题目给出的结论非常美妙。
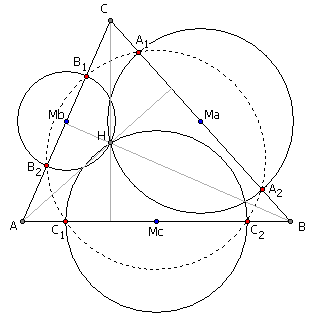
给定一个锐角三角形△ABC，垂心为H。Ma、Mb、Mc分别为三条边的中点。以Ma为圆心，过点H的圆与线段BC相交于点A1、A2；类似地，以Mb、Mc为圆心，过点H的圆与三角形交于B1、B2、C1、C2。求证，A1、A2、B1、B2、C1、C2六点共圆。
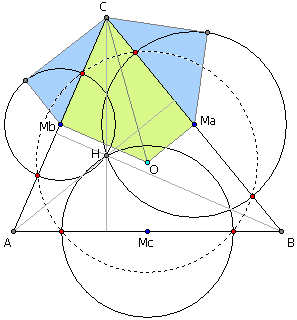
首先注意到，图中三角形的三条垂线正好穿过了圆和圆之间的公共弦。我们可以很轻易地证明这一点。只需注意到线段MaMb是三角形的中位线，它平行于AB，我们立即得到MaMb⊥HC；而过两圆交点并垂直于连心线的正好就是两圆的公共弦，因此圆Ma和圆Mb的公共弦在HC上。对于其余两对圆有同样的结论。由于C在圆Ma和圆Mb的公共弦的延长线上，因此C到两圆的切线一样长。假设这个长度为t。另外，把圆Ma和圆Mb的半径长分别记作Ra、Rb。观察两个蓝色的直角三角形，显然有(AC/2)^2 – (Rb)^2 = t^2 = (BC/2)^2 – (Ra)^2。
另一方面，如果题目中的六个点共圆，圆心一定在A1A2、B1B2、C1C2的中垂线的交点上（实际上也就是△ABC的外心）。假设这个点为O，它到Ma、Mb的距离分别为Sa、Sb。观察两个绿色的直角三角形，显然有(AC/2)^2 + (Sb)^2 = (OC)^2 = (BC/2)^2 + (Sa)^2。两式相减，有(Rb)^2 + (Sb)^2 = (Ra)^2 + (Sa)^2，应用到△OMaA1、△OMaA2、△OMbB1、△OMbB2四个直角三角形上，立即可以看到点O到A1、A2、B1、B2的距离相等，这四个点共圆。
同理，B1、B2、C1、C2也共圆，因此这六个点都在同一个圆上。
参考资料：http://www.cut-the-knot.org/Curriculum/Geometry/CirclesThroughOrthocenter.shtml
沙发～
根据老封的说法
用到了射影几何的东西
不就是六个点对于△ABC外接圆的幂都相等么，自然共圆
CB1 * CB2 – CA1 * CA2
= (CMb^2 – HMb^2) – (CMa^2 – HMa^2)
又因为 CH 垂直 MaMb ==> CMb^2 – HMb^2 = CMa^2 – HMa^2 ==> CB1 * CB2 = CA1 * CA2
同理……
不知LZ如何看这种做法……
根轴定理
想起来初中有个九点共圆的
自己想的方法
(R*sinA-b*cosC)^2+(R*cosA-b×sinC)^2
=R^2+b^2-2R*b*sinB=R^2+b^2-2R*b*cos(90-B)=R^2
同理有若干相似等式
外心到A1,A2,B1,B2,C1,C2距離相等
省略了許多,但熟悉幾何的朋友因該很快知道怎么列出這個的吧..
(AC/2)^2 – (Rb)^2 = t^2 = (BC/2)^2 – (Ra)^2
则有B1C*B2C == A1C*A2C，
此时为什么不直接判定A1A2B1B2四点共圆？
首先任意两圆交点都在垂线上面(中位线定理和弦的中垂线的什么定理)，所以那条垂线对应的定点出发，两次割线定理（中间那条公共弦就是公共割线），所以这4点共圆。。所以6点共圆。。。
《近代欧式几何》上有一个费尔巴哈圆，就是三角形三边的中点,三高的垂足和三个欧拉点（连结三角形各顶点与垂心所得三线段的中点）九点共圆。同样美妙。
CB1 * CB2 – CA1 * CA2
= (CMb^2 – HMb^2) – (CMa^2 – HMa^2)
又因为 CH 垂直 MaMb ==> CMb^2 – HMb^2 = CMa^2 – HMa^2 ==> CB1 * CB2 = CA1 * CA2
同理……
赞成这种做法
割线定理证四点共圆(用到中线长公式),毫无计算量可言(对我而言).
三组四点共圆,若均不同圆,由根心定理知三角形三个顶点共线.