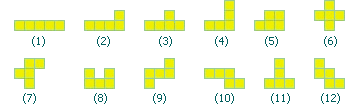
IBM Ponder This上个月的题目：一个多联骨牌(polyomino)是指平面上若干个正方形相接拼成的图形。经过旋转、镜像得到的图形仍然视为相同的多联骨牌。如上图所示，五联骨牌一共有12种。我们说一个多联骨牌A覆盖B，如果我们能在B上添加若干个新的方块得到A。回答下面两个问题：
    1. 一个六联骨牌最多可以覆盖多少种不同的五联骨牌？
    2. 给出一个最小的能够覆盖所有12种五联骨牌的图形。

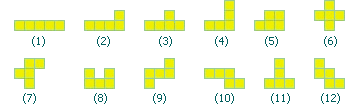
    1. 覆盖5种是不可能的。证明很容易：六联骨牌只有有限个，挨个枚举就是了。为了减小枚举量，我们对这个问题稍作分析。换个角度考虑：把六联骨牌的其中一个方块去掉，是否能保证得到5种不同的连通图？如果这个六联骨牌没有“环”的话（即对应的图是一棵树），那么除了叶子节点以外其余点都是割点，去掉后无法形成连通图；但6个节点的最大度为4的无根树最多只能有4个叶子，不可能弄出5种连通图来。这意味着这个六联骨牌必须要有环。而使用不超过6个方块就能得到的环只能是2×2的方形了，因此这个六联骨牌必然有一个2×2的方形。下面我们从2×2的方形出发，添加两个新的方块上去。由对称性，第一个方块拼接在什么位置无所谓，反正都是“刀板五”的形状。现在我们只需要考虑第二个方块的9种可能的位置（事实上不同的只有8种）。割点最多一个的图形只有两种，但它们都是对称图形，将会出现很多重复的情况。于是，我们看到，覆盖5种不同的五联骨牌是不可能的。妈的累死了，谁有更简单的分析方法没？
    下面给出两个可以覆盖4种五联骨牌的六联骨牌：

             #
####       ###
##         ##

    2. 8个方块显然是不够的。把长条形(1)和阶梯型(12)合在一起就已经需要至少8个方块了，而它们组成的形状显然无法覆盖十字架形(6)。下面给出两个九联骨牌的解：

 ###       ###
#####      #####
 #           #