在所有周长相等的长方形中,正方形拥有最大的面积;在所有周长相等的平面图形中,圆拥有最大的面积;在所有表面积相等的长方体中,正方体拥有最大的体积;在所有表面积相等的立体图形中,球拥有最大的体积。所有这类问题的答案都是越对称的图形越好吗? George Pólya 在 Mathematical Discovery 一书中的第 15 章里举了下面这个例子。
在给定圆周上选取四个点构成一个四边形,那么正方形的面积一定是最大的吗?答案是肯定的。只要有哪个点不在相邻两点之间的圆弧的中点处,我们都可以把它移动到这段圆弧的中点处,使得整个图形的面积变得更大。好了,我们现在的问题是,在球面上选取八个点构成一个顶点数为 8 的多面体,那么正方体一定是体积最大的吗?
答案居然是否定的。单位球中的内接正方体,体对角线将会等于球的直径 2 ,那么这个正方体的边长 x 就应该满足 x2 + x2 + x2 = 22 ,解得 x = 2 / √3 。因而,这个正方体的体积就是 (8 / 9) · √3 。现在,让我们再想象这样一种单位球中的内接多面体:作出赤道面上的内接正六边形,再把它的各个顶点与南北极相连,构成一种由两个正六棱锥拼接而成的立体图形。每一个正六棱锥的底面都是一个边长为 1 的正六边形,其面积为 (3 / 2) · √3 ;由于棱锥的高也是 1 ,因此棱锥的体积就是 (1 / 3) · (3 / 2) · √3 = (1 / 2) · √3 。两个这样的棱锥拼在一起,总体积就是 √3 ,这比单位球里的内接正方体体积更大。看来,在与几何图形相关的最值问题中,并不是最对称的那个图形就是最好的。
为什么会出现这种情况呢?其中一种原因是,立方体虽然非常对称,但它的面太少了。可以想象,如果两个多面体内接于同一个球里,并且它们的顶点数相同,那么谁的面更多一些,谁就有希望占据更大的空间。事实上,我们可以推出,对于顶点数目一定的多面体,如果面数达到最大,则每个面都将会是三角形。根据 Euler 公式,多面体的顶点数 V 、棱数 E 和面数 F 满足 E = F + V – 2 ,另外注意到多面体所有面的边数之和为 2 · E (因为每条棱都被算了两次),因而平均每个面的边数就可以表示为 2 · E / F = 2 · (F + V – 2) / F = 2 + (2 · V – 4) / F 。从这个式子中可以看出,当顶点数目一定时,随着面数的增加,多面体平均每个面的边数将会减少。面数最多的情况,也就是多面体平均每个面的边数最少的情况,也就是每个面都是三角形的情况。
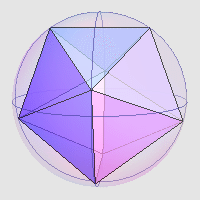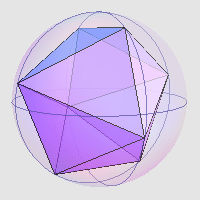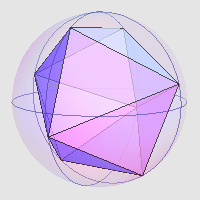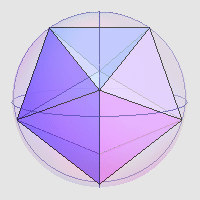
其实,刚才那个双棱锥仍然不是最优解。下图所示的单位球内接多面体也拥有八个顶点,但它的体积更大,约为 1.8157161 。根据我能查到的资料显示,这应该就是体积最大的解了。