有一道非常经典的智力问题：假设有两个一模一样的硬币 A 和硬币 B ，如果让硬币 B 不动，让硬币 A 贴着硬币 B 旋转一周，那么硬币 A 自身旋转了多少周？一个常见的错误答案是“显然也是一周啊”，而实际上正确的答案是两周，如下图所示。我们有很多方法来解释这种现象，其中最传统的说法便是“公转了一周，自转了一周”。硬币 A 的运动是由两部分合成的，公转一周（想像一个人绕着地球走了一圈），以及自转一周（想像一个轮子在地面上滚动了一周）。想像你是站在硬币 B 中心处的一个小人儿，看着硬币 A 贴着你脚下的硬币转动一圈。如果在此过程中，你始终面向硬币 A ，那么在你看来，硬币 A 似乎就是在长为 2πr 的平地上滚了一圈。而实际上，在观察硬币 A 的过程中，你自己也原地转了 360 度，因此从外面的人看来，硬币实际上转了两周。
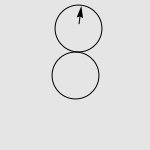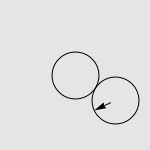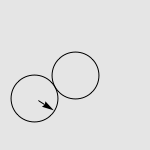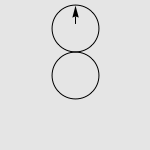
写了这篇文章后，我习惯性地开始用正多边形逼近的思路去分析一些与圆有关的一般性结论。在准备一份初中几何问题的材料时，我突然想到了上述问题的一个简单而漂亮的解释方法。
考虑一个正方形贴着另一个正方形旋转一周，你会发现，前者自身也旋转了两周。容易验证，对于正三角形和正六边形，情况也都是如此。这一定不是巧合，或许对于所有的正 n 边形，结论都同样成立。仔细一想，你发现这很容易理解：对于正 n 边形来说，每转过一个顶点，转过的角度都相当于正 n 边形两个外角的大小。转过 n 个顶点回到出发位置后，正 n 边形显然转过了两倍的外角和，也就是 720 度。因而，正 n 边形自身旋转了两周。当正多边形的边数趋于无穷多时可知，一枚硬币贴着另一枚硬币旋转一周，则这枚硬币自身也一定正好旋转了两周。
sf
2F
用物理学相对运动的观点非常好解释，而且可以扩充到绕一个比自己大的圆周运动或者比自己小的圆周上：
两圆r和R，相对运动一周，经过的长度为为2pie*(r+R)；
现取其中一圆r为参考系，那么另一圆R运动所经过的长度即为2pie*(r+R)；
对应自身的旋转即为运动了（r+R）/R 圈。
r=R，2；
r=2R，3；
r=无穷大，无穷大；
r=无穷接近0，1；
这也用不着正多边形吧……随便一对镜像对称的图形就行……图形转了一圈，镜面本身也转了一圈。
哈 有意思。
有错别字哦……：“……因此从外面的人‘开’来……”
回复：谢谢指正，已改
初中时候为了做参考书上的这道竞赛题，特意在晚自习（有老师巡查）花大力气借了两枚硬币，两个人合作转了半天……
前排围观
地核是我的。
～和对称性以及群论可能有关系。另外两个圆的半径大小不同，结果可能不一样；此外，相对运动当然可以解决所有问题。对于转动的球来说，取他的质心为参考性，自身在旋转；实际其质心也在旋转。不同参考系位移（和）具有不变性，于是就是2倍数了。
把A、B两个圆的周长设为2∏r和2∏R的线段，把A圆围绕B圆旋转一周看成A线段通过B线段所走的距离，这样的解释更简单吧，适合任何旋转吗？
常见的错误认为旋转一周，那是因为把A圆看成一个点围绕B圆旋转一周的公转周期；看成一个线段的话A线段重合B线段的一周是公转周期，A线段离开B线段的一周是其自转周期。
加入连个圆的半径不同呢 具体外圆转了多少角度应该如何计算
11楼的解释也不错
也可以由物理上无滑纯滚观点来看，旋转的硬币自身圆心角速度ω，旋转硬币圆心绕静止硬币圆心角速度Ω，硬币的半径设为R。
由于作无滑纯滚，可以列方程Ω(R+R)=ωR所以ω=2Ω：贴着另一枚硬币旋转了一周的硬币自身旋转了两周；
还可以这样处理半径不一样的两枚硬币，设静止硬币半径R，运动硬币半径r
Ω(R+r)=ωr所以ω=(R+r)Ω/r：贴着另一枚硬币旋转了一周的硬币自身旋转了(R+r)/r周
把中间的硬币的边拉直了是转一圈
所以为什么是2圈，其实其中有一圈是算在“脚下的大地”上面的
这样解释可以意会，没法更加具体了。不知道高人能不能给解释一下。
其实可以接着考虑两个半径不同的硬币A、B，A绕着B转动一周情况下自身转动几周
赶脚最好理解的应该是从位移上去理解。此时外圈的硬币的位移是4πr（如果用点抽象的话，外圈硬币应该是距离内圈硬币重心2r处的点，而位移就是半径为2r的圆周），而硬币的周长是2πr。
以A中心为圆心，A到B的距离为半径做圆。A自己的半径为r，AB圆半径为2r，则实际走过的距离是两倍，
假设轮子周长10厘米，轮子自转一圈，那么小车就前进10厘米。即滚圆的圆心的运动路程等于滚圆上的点绕滚圆的圆心自转的路程。本题中滚圆的圆心的运动路程2兀d，所以滚圆上点自转了2兀d/兀d=2周。
若中心圆的半径是kr,可用类似的办法求得小圆转了k+1圈，多边形的方法神奇！
这个很有趣啊，关注度很高嘛，很有意思
哪位大牛能给我解释一下怎么算“自身旋转一周”？
想博文中这种情况算旋转两周？
像月球绕地球那种情况（有一点始终朝向地球），算旋转一周？
如果A硬币只有公转没有自转（平移），算旋转零周？
公转一周自转一周？
我感觉是公转一周自转两周啊？
然后公转的其实是没有用的，自转的才算圈啊！
就11楼看懂了 T T
完全无法理解，“自身旋转了多少周”难道不是指边上任意一点相对于圆心的自转？
旋转了多少周？
＝＝＝＝＝
开始认为是2周，看了图以为是1周，再看文章是2周。
这个旋转＋1周有歧义啊：1：角度：转过了360度；2：长度：走过了一周的周长
初中一道考试题上遇到了这个选择题 我觉得好奇怪 后面用硬币转了一下 貌似是一周啊 怎么2周呢…
计算圆转一周方法是2PI*R，如果A绕B一周，也可以当做计算一个圆的周长，但是这个圆就是以B的圆心为圆心，A的圆心为半径的圆，周长即为4PI*R。由此，A绕的圈数为2.
类比一下：
（1）如果让一个圆在直线上转动一圈，发现圆心平动了2pi*r(这是个逆否命题)
(2)此题当中动圆绕定圆旋转一周（始终保持外切），这时发现外圆的圆心总共移动了4pi*r。相当于外圆在直线上滚动，圆心平动了4pi*i，即此圆转动两圈。
空间变换会不会更直观？
其实问题忽略了一个条件，就是只考虑了静摩擦的情况，如果两个硬币间存在滑动摩擦，那么结果就不一定了。这时自转频率不等于公转频率
不太明白，什么叫硬币转了一圈？如果说相对于圆心，圆周上正北方向的一点经过运动后又回到了圆心的正北方向，这叫转了一圈。那么结论明显就是一圈嘛。
为啥刚才的评论显示不了？
我觉得这个问题有更一般的模型：一个圆沿着和它时刻相切的任意轨道y=f(x)滚动。这个过程中，圆转过的角度 = 该圆走过的路径 / 该圆的半径。当轨道是连续曲线弧时，可以用定积分求走过的路径。而轨道是相同半径的圆只是该情况的特例。
感谢大神！fdu的面试刚好问到这个问题，哦呵呵，我“略一思索”就自己“想”出来噜。。。
lz贴的方法与我第一次做这个的方法一致，在贴个更简单的解释，就拿1:1为例吧，把静圆拉直，动圆走完肯定是一圈，先在想象动圆走的时候，线段也开始形成静圆，即一端固定标个箭头，另一端上也标个同方向箭头，动圆一直在追赶动的一端，箭头再次同向的时候动圆也多走转了一圈，在加上长度的那圈就是两圈了。
如果把B的圆周抻直了的话，A的圆心走了2pi*R的距离。所以……
lz，我也想到过相关的问题，考虑将一个多边形旋转一周（360°），可以得到多边形外角和是360°~~这是比(n-2)×360°-n×360°直接得多的做法。
我想的是 如果把两个硬币考虑成两个紧贴并且向相反方向滚动的圆盘(类似两个同样直径的齿轮结合在一起) 那么其中一个滚动一周另一个也就朝相反方向滚动了一周 如果其中一个做为固定不动的参照物 那么另一个也就滚动了两周 木有数学建模能力的肉脑思考星人路过..
11楼完解，任何旋转。
11楼不太理解啊…
11楼的解法不怎么理解啊，还是用相对运动的观点解释好懂
个人理解（不同于楼层：地毯）
用相对运动的观点，以r为半径的圆b为参考，按照题目来说，半径为R圆a绕b一圈结束时，经过的总长度为2*(2pie*r)，所以对于a来说旋转的圈数位2r/R圈 （R、r！=0）
求指导我错在哪？或者地毯错在哪？谢谢
1.问半径为R的圆沿着半径为4R的圆内侧无滑滚动一周转过的圈数与沿着4R的圆外侧无滑滚动一周所转过的圈数是否相同？（两者圆周走过的距离一样。）
2.问半径为R的圆沿着半径为4R的圆内侧无滑滚动一周转过的圈数与沿着2R的圆外侧无滑滚动一周所转过的圈数是否相同？（两者圆心走过的距离一样。）
1.问半径为R的圆沿着半径为4R的圆内侧无滑滚动一周转过的圈数与沿着半径4R的圆外侧无滑滚动一周所转过的圈数是否相同？（两者圆周走过的距离一样。）
2.问半径为R的圆沿着半径为4R的圆内侧无滑滚动一周转过的圈数与沿着半径2R的圆外侧无滑滚动一周所转过的圈数是否相同？（两者圆心走过的距离一样。）
11楼的解释很不错
直接不用多想。。。。
假设两个都会动，那么每个走一周，刚好是都回到原点，那么当一个静止的时候，另一个的相对路程就是2倍了。
11楼的解释是非常棒的 把圆化成线段能更好的理解
其实这个问题十分简单，即角速度和线速度之间的关系。v=wR
所以自转同一周，同时完成公转一周可以视为自转圆圆心行程问题。同时两圆角速度是相同的，所以线速度v1/v2=R1/R2.
说个题外话，自转圆周上某点的运动路线谁知道是怎样的吗？
感谢感谢啦
赞一个
本质上这只是一个几何问题，通过几何方法就可以解决。问题的关键是A圆上的点始终是B圆的镜像，所以在任意位置都可以通过A、B两个圆切点所在确定A圆上任意点经过相对于A圆的圆心的角度变化。如切点相对B圆变化x度，那么A圆上的任意一点也相对A圆变化x度，做一条平行线，可以得出A圆变化了x+x=2x。
哈哈，这个多边形的解释，属于作者陷入自己心理学上的虫洞了。其实，三角形和多边形，只要考虑一个问题就够了，也就是最开始贴合的那个面，是此多边形的镜像的同一个面，转一圈回来之后，这两个面没有和任何其他面接触，还是贴合在一起，这已经是自转一圈的证明了。
如果是两个大小不一的圆呢？我觉得是（路径长/小圆周长）+1次，大神指导。
为了验证，我和朋友做了个实验：
首先我们用脚底贴着对方的脚底平躺着，现在我们还是线段状态
然后我们把头尽力靠向各自的脚，我们就成了两个圆。
接下来我把头靠在朋友的头上，沿着他的脊背做了个前滚翻，此时我旋转了360°，但并没有回到一开始头靠头的姿势，而是变成了菊花靠菊花。我知道这是不对的，我还得再转360°，可朋友没给我完成实验的机会—-他感觉到了什么，异常兴奋，箭一样冲出门去了。
我的想法是 外面的圆的圆心走过的路程是4piR 而对于纯滚动的圆来说 质心速度等于其上任何一点在质心系里的线速度，对于外面的圆上的点来说 也是走过了4piR 所以转了两圈
从圆心考虑还是好理解的。
理论力学基本问题：纯滚
外面的硬币走的距离等于其质心（此处即圆心）运动的距离，即2π*（R+R）,硬币半径为R故运动了两圈
学点力学这题就很容易理解了
很有收获啊
这个多边形的解释，属于作者陷入自己心理学上的虫洞了。其实，三角形和多边形，只要考虑一个问题就够了，也就是最开始贴合的那个面，是此多边形的镜像的同一个面，转一圈回来之后，这两个面没有和任何其他面接触，还是贴合在一起，这已经是自转一圈的证明了。
这个方法在数学上有个明显的错误：设圈数为f（n），则任意n，f（n）=2成立，但是这不能得出lim(n–>正无穷)f（n）=f（正无穷），f这个函数对于极限运算是否可交换你是不知道的。（这与一个收敛的连续函数列的极限函数未必收敛是一个道理）
动球质心运动路径长2PI*(R+r），是运动通过滚动实现，即动球滚动了2PI*(R+r）=2PI*r*n
搞这么复杂？设外圆圆心相对切点的转动角速度是a，切点相对内圆圆心转动角速度也是a,则外圆圆心相对内圆圆心（不动点，是我们观察者的参考系）的转动角速度是2a,自然就是2倍啦。
发现了一个好博客，分享
还行 看懂了
说句实在话，这已经不是数学问题，而是语文问题了，怎么定义自身旋转？莫怪我讲的难听，这是初高中数学的毛病，连个公理系统都没有，基本假设也没有就讨论问题，到最后肯定是谁有解释权谁正确。谁告诉你三角形的内角和是180度了？
回 xgs 的问题:
1. 否。沿内侧 =3 turns, 沿外侧 = 5 turns
2. 是。
自转一周，公转一周，只算自身旋转只能算一圈
有意思！
区别成功与失败者，是看他敢于冒险不。
很明显B移动的路程长度是B圆心经过的路程长度 而不是A的周长
这样一看就很好理解了。
谁能解释下这个问题 https://zhidao.baidu.com/question/1117361941729966139.html
大圆半径为2，固定不动，小圆半径为1，速度为1圈/秒,分别在大圆外部和内部无滑滚动一圈回到原点(起点)，问下分别用时是多少？这怎么计算？