有一个半径为 10 米的圆形舞台，初始时舞台上的某个地方有一头狮子。这头狮子在舞台上以折线段的方式跑了 30 千米。求证：在整个过程中，这头狮子至少转了 2998 个弧度。
有时候，换一个角度思考，问题就会迎刃而解。
现在，让我们站在狮子的角度，用狮子的眼光来看周围的世界。这样的话，狮子本身就是静止不动的，运动的其实是整个舞台；再假设狮子的头也是始终朝北的，狮子原地旋转实际上就是整个舞台绕着它做圆周运动。这样一来，舞台中心的运动就只有两种形式：竖直向下的直线运动，以及以狮子为中心的圆弧运动。如下图，左图就是在我们看来，狮子的移动轨迹，其中圆心代表舞台中心；右图就是在狮子的眼中，舞台中心的移动轨迹，其中圆心代表狮子。注意到，由于舞台始终包含了狮子，因此舞台中心绝不可能跑出狮子周围 10 米的范围。因此，每段直线运动都不能持续太久。我们需要不断靠圆弧运动上调舞台中心的位置，让它有继续竖直向下移动的空间。
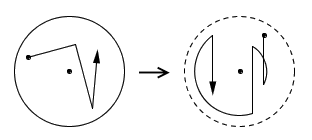
由于舞台中心一共下降了 30000 米，但舞台中心的初始位置最多只能比终点位置高出 20 米，因而在整个过程中，舞台中心的高度至少还要靠圆弧运动上调 29980 米。因此，圆弧运动的总路程也就至少有 29980 米（事实上，由于两点之间直线段最短，走弧线绕了弯路，因此实际路程比 29980 米大得多）。如果每段圆弧的半径都是 10 米，那么所有圆弧的度数之和就应该有至少 2998 弧度；何况绝大多数圆弧的半径都小于 10 米，因此圆弧的总度数就更大了。这就说明了，在整个过程中，狮子至少转了 2998 个弧度。
有意思。。。不然的话不容易计算
前排
前排 留言 再来看文章
昨天在renrenInc又见到m牛了。。。哈第二次见面咯
这不就是个鸽巢原理嘛
有点意思～
呵呵，算流水问题考虑船不动岸动的题差不多啊
interesting
这个题目有点意思
我思考了一下觉得这题目不用这么麻烦，首先走一个直径20m,然后就沿着圆上走，此时走的时候单位距离弧度少，所以是29980/10=2998，其实此时是一种极限，每一步很小，所有的步加起来看似接近圆。
有问题呀 ，如果直接在一个半径的上做运动，不经过圆心的话，那么不管走多少公里，走过的弧度为零呀
当狮子方向处于圆弧的切线上的时候，它必须转向，设转向的弧度为x.而转向之后沿着直线走到圆弧上是最经济的，否则又要转向。设这段距离为y。 y = 10 * sinx。sinx/x，在x趋向于0的时候，极限为1。也就是说转动的角度越小，单位弧度走过的距离最大。所以说狮子先沿着直径走20米，然后沿着圆弧走，可以得到这个下确界2998。
回复：小木云，你说的是这个意思吧？
不过这个证明过程有些繁琐，倒是不如matrix67的简单明了
是的，呵呵。@王凌云
对于学过高等数学的，我觉得我这种方法很简明易懂，反而我觉得M67的方法换一个参考系，我倒是开始反应不过来了，呵呵。@王凌云
@康乐 折线段的定义：用线段依次连接不在一直线上的若干个点所组成的图形。
我觉得应该大于2998个弧度，因为走到边缘的时候要先旋转90°，然后舞台才能进入正轨开始做圆周运动
@康乐180℃ ？
我觉得按照M67牛的方法不如直接想象成把狮子朝一个方向跑和另一个方向跑分开，两个方向各自都拼起来形成一圈一圈的圆，这样比较好
妙哉！
狮子转2π最多走一圆周，30000/(2π*10)*2π=3000个弧度，故最少走3000个弧度。……我是这样认为的……
好难啊 ……
弧度还是圈数？
。。。。。
这个题目有bug，关键是无法定义清楚什么叫做转过的弧度。
狮子走一条直径怎么算转过的弧度？
如果承认是0，那么可以让狮子反复走直径，每走一次稍微走个短弦，只要短弦跟直径比例充分小，转弧度的部分也就充分小，下略。
呃，重新看了一下，题目里说了狮子只跑线段，那么应当承认题目没错。
很好，很强大！！！
“换一个角度思考”的极佳范例！
比较同意20楼的观点。因为相同长度的线段，离圆心越远的所占的弧度越小；因此比较紧的下界应该是贴着圆周。又根据三角形两边之和大于第三边的定理和极限思想，贴着圆周走才是最紧的下界。
2998显然是不对的，因为作者没有考虑狮子位于舞台顶端时，舞台无法直接作近圆周运动，即狮子在舞台一段沿直径走到另一端时，需要先转向pi/4弧度才能开始近圆周运动。所以答案应为3000，即初始位置为舞台边缘且朝向为切线方向，然后一直做近圆周运动。
不是吧，狮子可以一直上下来回的跑啊，这样弧度不就为0了吗？