这次的趣题来源于 UyHiP 今年八月份的谜题:概率均等地随机选取一个恰好含有 n 个 0 和 n 个 1 的 2n 位 01 串,这个 01 串平均会有多少个 0 和 1 个数相等的前缀(包括空串和整个串本身)?
为了叙述简便起见,下面我们把所含 0 和 1 个数恰好相等的 01 串叫做平衡的 01 串。例如, 010010110011 就是一个平衡 01 串,它有四个平衡前缀,空串、 01 、01001011 以及整个 01 串本身。我们需要求出的就是,任取一个长为 2n 的平衡 01 串,平衡前缀的个数的期望值是多少。
注意到,在所有长为 2n 的 01 串中,平衡 01 串一共有 C(2n, n) 个。下面我们证明,所有这些串的所有平衡前缀一共有 4n 个,从而得出问题的答案,即 4n / C(2n, n) 。
不妨把所有 2n 位平衡 01 串的所有平衡前缀的总数记作 F(n) ,容易得出:
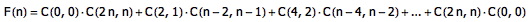
利用生成函数,我们可以瞬间证明,这个和等于 4n 。由 Taylor 展开可知, 数列 C(2n, n) 所对应的生成函数为:
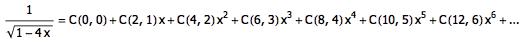
对上式平方,有:
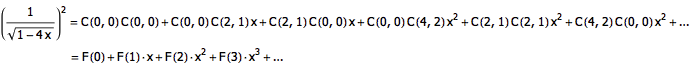
但
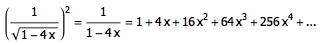
因此 F(n) = 4n 。
Joseph DeVincentis 和 Daniel Bitin 给出了一个初等的证明。令 S 为某个平衡 01 串,令 k 为 S 的某个平衡前缀的长度( k 有可能取 0 或者 2n )。我们下面建立一个从所有可能的 (S, k) 到所有长为 2n 的 01 串的一一对应的关系,从而说明所有平衡前缀一共有 4n 个。
我们先给出把 (S, k) 变换为一个普通 01 串的方法。首先,取 S’ = S 。接下来,找出 S’ 中比 k 更长的平衡前缀中最短的那一个,把它的长度记作 l 。然后,对 S’ 中从第 k + 2 位到第 l 位的数字全部取反。继续寻找新的 l 并执行相应的取反操作,直到 S’ 中不再有比 k 更长的平衡前缀。
下面我们来说明,这个过程不会无限继续下去,总会有终止的时候。不妨假设 S 的第 k + 1 位是一个 0 。由于取反操作不影响前面 k + 1 位数字,因此 S’ 的前 k 位始终平衡,第 k + 1 位也始终是 0 。容易看出,每次取反前,第 k + 2 位到第 l 位中 1 的个数比 0 的个数多一个,因此对这一段数字取反将会让整个串少一个 1 多一个 0,从而让整个串的后半部分越来越不平衡。因此,总有一个时候,第 k 位以后将会不再有别的平衡点产生。如果 S 的第 k + 1 位是 1 ,类似的推理同样成立。
然后,我们需要说明,这个对应关系确实是一一对应的。为此,我们需要给出把 S’ 变回 (S, k) 的方法。首先,我们可以很快还原出 k 的值来:找出 S’ 中最长的平衡前缀,它的长度就是 k 。注意, k 一定是偶数,并且有可能是 0 或者 2n 。如果 k 是 2n ,即 S’ 本身就是一个平衡串,那么我们可以直接还原出 S = S’ 。下面只考虑 k < 2n 的情况。 不妨假设 S' 的第 k + 1 位是 0 ,由于在此之后 S' 没有其他平衡点了,因此从第 k + 2 位开始数下去, 0 的个数必须始终大于等于 1 的个数。由于从第 k + 2 位一直数到最后一位一共有奇数个数字,因此其中 0 的总个数也就一定严格大于 1 的总个数。找出从第 k + 2 位起, 0 的个数首次超过 1 的个数的地方,比如说第 l 位。对第 k + 2 位到第 l 位的数取反(此时 S' 的前 l 位将变成一个平衡前缀)。这样一来,整个串的后面部分将会少一个 0 多一个 1 ,但 0 的个数有可能仍然比 1 多。继续找出从第 k + 2 位起首次 0 的个数刚好比 1 多一个的地方,像刚才那样继续取反,让 0 越来越少, 1 越来越多,直到整个串变为平衡串为止。整个过程显然是从 (S, k) 变换到 S' 的逆操作,因而最后得到的串正是 S 。当然,如果 S' 的第 k + 1 位是 1 ,上面的推理同样成立。至此,我们便完成了全部证明。