数学猜想并不总是对的,错误的数学猜想不占少数。关键在于,有时反例太大,找出反例实在是太困难了。这篇日志收集了很多“大反例”的例子,里面提到的规律看上去非常诱人,要试到相当大的数时才会出现第一个反例。
千万不要迷信规律
圆上有 n 个点,两两之间连线后,最多可以把整个圆分成多少块?
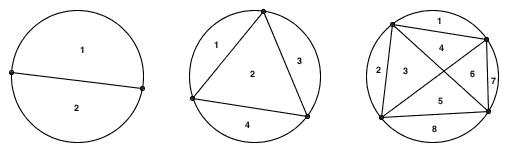
上图显示的就是 n 分别为 2 、 3 、 4 的情况。可以看到,圆分别被划分成了 2 块、 4 块、 8 块。规律似乎非常明显:圆周上每多一个点,划分出来的区域数就会翻一倍。
事实上真的是这样吗?让我们看看当 n = 5 时的情况:
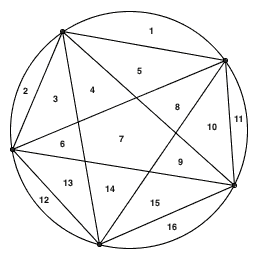
果然不出所料,整个圆被分成了 16 块,区域数依旧满足 2n-1 的规律。此时,大家都会觉得证据已经充分,不必继续往下验证了吧。偏偏就在 n = 6 时,意外出现了:
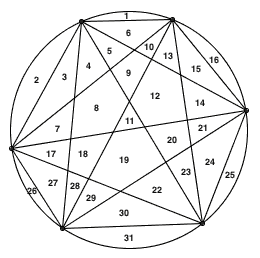
此时区域数只有 31 个。
最有名的素数生成公式
1772 年,Euler 曾经发现,当 n 是正整数时, n2 + n + 41 似乎总是素数。事实上,n 从 1 一直取到 39,算出来的结果分别是:
43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281,
313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853,
911, 971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601
这些数全都是素数。第一次例外发生在 n = 40 的时候,此时 402 + 40 + 41 = 402 + 40 + 40 + 1 = (40 + 1)(40 + 1) = 41 × 41。
xn – 1 的因式分解
x2 – 1 分解因式后等于 (x + 1)(x – 1) 。 x20 – 1 分解因式后等于
(x – 1) (x + 1) (x2 + 1) (x4 – x3 + x2 – x + 1) (x4 + x3 + x2 + x + 1) (x8 – x6 + x4 – x2 + 1)
对于所有的正整数 n , xn – 1 因式分解后各项系数都只有可能是 1 或者 -1 吗?据说有人曾经算到了 x100 – 1 ,均没有发现反例,终于放心大胆地做出了这个猜想。悲剧的是,这个猜想是错误的,第一个反例出现在 n = 105 的情况, x105 – 1 分解出来等于
(x – 1) (x2 + x + 1) (x4 + x3 + x2 + x + 1) (x6 + x5 + x4 + x3 + x2 + x + 1)
(x8 – x7 + x5 – x4 + x3 – x + 1) (x12 – x11 + x9 – x8 + x6 – x4 + x3 – x + 1)
(x24 – x23 + x19 – x18 + x17 – x16 + x14 – x13 + x12 – x11 + x10 – x8 + x7 – x6 + x5 – x + 1)
(x48 + x47 + x46 – x43 – x42 – 2 x41 – x40 – x39 + x36 + x35 + x34 + x33 + x32 + x31 – x28
– x26 – x24 – x22 – x20 + x17 + x16 + x15 + x14 + x13 + x12 – x9 – x8 – 2 x7 – x6 – x5 + x2 + x + 1)
以 2 为底的伪素数
下面是当 n 较小的时候, n 与 2n – 2 的值。
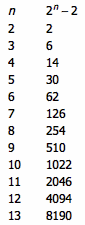
似乎有这样的规律: n 能整除 2n – 2 ,当且仅当 n 是一个素数。如果真是这样的话,我们无疑有了一种超级高效的素数判定算法( 2n 可以用二分法速算,期间可以不断模 n )。国外数学界一直传有“中国人 2000 多年前就发现了这一规律”的说法,后来发现其实是对《九章算术》一书的错误翻译造成的。再后来人们发现,这个规律竟然是错误的。第一个反例是 n = 341,此时 341 能够整除 2341 – 2 ,但 341 = 11 × 31 。
事实上,根据 Fermat 小定理,如果 p 是素数,那么 p 一定能整除 2n – 2。不过,它的逆定理却是不成立的,上面提到的 341 便是一例。我们把这种数叫做以 2 为底的伪素数。由于这种素数判定法的反例出人意料的少,我们完全可以用它来做一个概率型的素数判定算法。事实上,著名的 Miller-Rabin 素性测试算法就是用的这个原理。
Perrin 伪素数
定义 f(n) = f(n – 2) + f(n – 3) ,其中 f(1) = 0 , f(2) = 2 , f(3) = 3 。这个数列叫做 Perrin 数列。
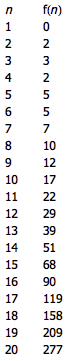
似乎有这么一个规律: n 能整除 Perrin 数列的第 n 项 f(n) ,当且仅当 n 是一个素数。如果这个规律成立的话,我们也将获得一个效率非常高的素数检验方法。根据 MathWorld 的描述,1899 年 Perrin 本人曾经做过试验,随后 Malo 在 1900 年, Escot 在 1901 年,以及 Jarden 在 1966 年都做过搜索,均未发现任何反例。直到 1982 年, Adams 和 Shanks 才发现第一个反例 n = 271 441 ,它等于 521 × 521 ,却也能整除 f(271 441) 。下一个反例则发生在 n = 904 631 的时候,再下一个反例则是 n = 16 532 714 。这种反例被称为 Perrin 伪素数。
最经典的大反例
说到大反例,这是我最喜欢举的例子。下面是大于 1 的正整数分解质因数后的结果:
2 = 2
3 = 3
4 = 2 × 2
5 = 5
6 = 2 × 3
7 = 7
8 = 2 × 2 × 2
9 = 3 × 3
10 = 2 × 5
…
其中,4、6、9、10 包含偶数个质因子,其余的数都包含奇数个质因子。你会发现,在上面的列表中一行一行地看下来,不管看到什么位置,包含奇数个质因子的数都要多一些。1919 年,George Pólya 猜想,质因子个数为奇数的情况不会少于 50% 。也就是说,对于任意一个大于 1 的自然数 n ,从 2 到 n 的数中有奇数个质因子的数不少于有偶数个质因子的数。这便是著名的 Pólya 猜想。
Pólya 猜想看上去非常合理——每个有偶数个质因子的数,必然都已经提前经历过了“有奇数个质因子”这一步。不过,这个猜想却一直未能得到一个严格的数学证明。到了 1958 年,英国数学家 C. B. Haselgrove 发现, Pólya 猜想竟然是错误的。他证明了 Pólya 猜想存在反例,从而推翻了这个猜想。不过,Haselgrove 仅仅是证明了反例的存在性,并没有算出这个反例的具体值。Haselgrove 估计,这个反例至少也是一个 361 位数。
1960 年,R. Sherman Lehman 给出了一个确凿的反例:n = 906 180 359。而 Pólya 猜想的最小反例则是到了 1980 年才发现的:n = 906 150 257。
Fermat 大定理还能推广吗?
Fermat 大定理说,当 n > 2 时,方程 xn + yn = zn 没有正整数解。 Euler 曾经猜想,当 n > k 时,方程 x1n + x2n + … + xkn = yn 都没有正整数解。 1986 年,Noam Elkies 给出了方程 x4 + y4 + z4 = w4 的一个正整数解,从而推翻了这个猜想。这个反例是:2 682 4404 + 15 365 6394 + 18 796 7604 = 20 615 6734 。
XX 型平方数
11, 22, 33, 44, 55, 66, 77, 88, 99, 1010, 1111, 1212, … 都不是完全平方数。有没有什么数,把它连写两次后,正好是一个完全平方数呢?有。第一个这样的数是 13 223 140 496 ,把它连写两次将得到 1 322 314 049 613 223 140 496 ,是 36 363 636 364 的平方。第二个这样的数则是 20 661 157 025 ,它对应了 45 454 545 455 的平方。更多信息可见 http://oeis.org/A102567 。
总是相等吗?
下面是 n 为正整数时, 2 / (21/n – 1) 取上整的结果与 2n / ln(2) 取下整的结果:

这两者的结果总是相等吗?不是的。第一个反例是 n = 777 451 915 729 368,前者算出来的结果是 2 243 252 046 704 767 ,但后者是 2 243 252 046 704 766 。下一个反例则出现在 n = 140 894 092 055 857 794 的时候。更多信息可见 http://oeis.org/A129935 。
至今仍未找到的反例
有没有什么猜想,明明已经被推翻了,所有人都知道存在反例,但因为反例实在是太大了,直到现在仍然没有找到呢?有。下面这张表展示了 n 取不同值时 pi(n) 和 li(n) 的值,其中 pi(n) 表示不超过 n 的素数的个数,li(n) 则是对数积分 ∫0n dx/ln(x) 。
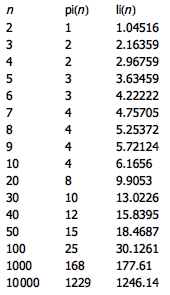
pi(n) 是否永远小于 li(n) 呢?1914 年,Littlewood 证明了存在一个大数 n 使得 pi(n) ≥ li(n) ,不过却并没有给出一个具体的 n 值来。1955 年,Skewes 给出了这样的 n 值的一个上界:在 10^(10^(10^963)) 以内,必有一个满足 pi(n) ≥ li(n) 的 n 。
虽然数学家们正在不断地改进上界(目前的上界大约是 e727.9513 ),但仍然无法找出一个具体的 n 来。原因很简单——这个反例实在是太大了。
几个主要来源:
http://redd.it/iikk4
http://www.guokr.com/article/9688/
http://mathoverflow.net/questions/15444
如果你对此感兴趣,不要错过数学史上的一篇经典论文:The Strong Law of Small Numbers
这篇日志今后将不断更新
2011-10-13 Update:
Borwein 积分
2001 年, David Borwein 和 Jonathan M. Borwein 在一篇论文中指出:
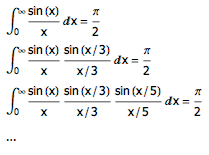
事实上,这个规律一直到
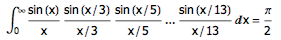
都是成立的。但
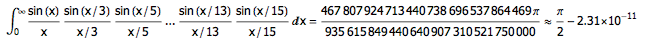
却打破了规律。其原因是, 1/3 + 1/5 + … + 1/15 超过了 1 。