看看自己脚下的地板——虽然正方形、长方形、正六边形等图形都能平铺整个平面，但平铺的方式却非常无聊，不过是同一种模式不断重复罢了。有没有什么“非平凡”的平铺方案呢？下面就给大家看这样一个图形，加上一些限制条件之后，它仍然能够平铺整个平面，不过平铺出来的结果却非常神奇——它并不能通过简单的重复得到，也就是说它不具有周期性。
下图就是这个传说中的地板砖（及其镜像）：
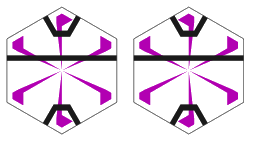
拼接时有两个要求：
(1) 黑色的线条必须连在一起
(2) 一条边两端的紫色小旗必须朝向相同的方向（如箭头所示，注意两个小旗来自于两个不相邻的砖块）
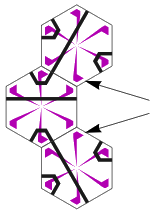
可以证明，用这种六边形（及其镜像）是能够平铺整个平面的，但方案是唯一的——一个有点分形味道的图形。拼接的限制很巧妙地迫使黑色线条构成规模越来越大的三角形，从而使得整个图形在任意方向上都不具有周期性。
这是首个用单块图形实现的只能非周期地平铺整个平面的砖块，是由 Joan M. Taylor 在今年 9 月发现的。详细的讨论可以看看 他的论文 。
很神奇~~
哎呀~差点沙发~
谢尔宾斯基三角形！ 神奇啊！
想起某桌游了～
想起很久以前某道题了……
朋友介绍来看这个帖子，蛮有趣的。让我想起自己做喜欢的桌游tantrix了。我在这里也发了2个帖子，关于马赛克，有机会看下。多交流。
http://tantrixchina.com/?p=303
http://tantrixchina.com/?p=429
很想看见宏观的大图，那样才比较有感觉
很有趣，尤其是因为其实一块砖包含的信息不多。他只有6个位置选项。而他的位置信息则是独一无二的。。感觉从这一点能引发很多思考。。
Like
像万花筒。
而且还存在砖块的配置，使判断其能否铺满整个平面是个不可解问题。
呵呵……这地板不错……
为什么我想到了分形，这不就是那个三角形的一部分么
我想起那个用两种砖头拼成非周期图案的。
看起来像中心对称的五边形
现在，我的问题是：
如果在球面上呢？砖头应该是什么样的
awesome！！
以后会常来Matrix67大牛的博客的，都是一些新鲜的东西，很受益^__^
请问这和彭罗斯镶嵌有什么联系么？
对啊，17楼说的是，我正在看彭罗斯的《皇帝新脑》，提到这个的
感觉很奇特!呵呵!
to 19l
我也是看的那本啊，前面的图灵机有点难懂，后面的好些。
下面连接了很多瓷砖的广告阿
Matrix67，你好。
我有个问题想请教你一下：
k个相同的盒子等间隔放在转盘上，将n个相同的球放到这些盒子里（盒子可以为空），有多少种放法。
这个与一般的问题差别在：盒子是环排列的，既不是完全无序，又不是各不相同。
我自己想了很长时间，也没想出来。在网上也没搜到。
希望你能看一下，谢谢了！
Matrix67，你好。
我有个问题想请教你一下：
k个相同的盒子等间隔放在转盘上，将n个相同的球放到这些盒子里（盒子可以为空），有多少种放法。
这个与一般的问题差别在：盒子是环状排列的，既不是完全无序，又不是各不相同。
我自己想了很长时间，也没想出来。在网上也没搜到。
希望你能看一下，谢谢了！
这Ideal亮
“但方案是唯一的”这说法有误。可以证明，至少存在两种在任何意义上都不相同的方案，其中一种存在一根无限长的黑色直线，另一种不存在。
有兩個相關網頁，在這分享
http://www.tilings.org.uk/shapes/
http://www.mathematicians.org.uk/eoh/tap/
你觉得可以平铺吗！
我自己想了很长时间，也没想出来。在网上也没搜到。