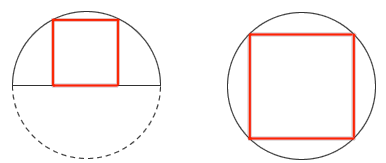
在半径相等的半圆和圆中各画一个内接正方形。这两个正方形的面积之比是多大?有什么简单些的算法吗?
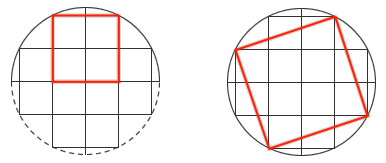
答案:两个正方形的面积之比是 2:5 。考虑 12 个单位小正方形排成的一个十字架,以及这个十字架的外接圆。半圆里的内接正方形占了其中 4 个单位小正方形,而圆内接正方形的边长则是 √10 ,它的面积就为 10 。因此,两个正方形的面积之比就是 2:5 。嚯嚯,秒杀咯!

在半径相等的半圆和圆中各画一个内接正方形。这两个正方形的面积之比是多大?有什么简单些的算法吗?

答案:两个正方形的面积之比是 2:5 。考虑 12 个单位小正方形排成的一个十字架,以及这个十字架的外接圆。半圆里的内接正方形占了其中 4 个单位小正方形,而圆内接正方形的边长则是 √10 ,它的面积就为 10 。因此,两个正方形的面积之比就是 2:5 。嚯嚯,秒杀咯!