不走寻常路：寻找线段的中点

    一名初三的学生刘小坤给我提出了这样的问题：

给你一条线段 AB ，再预先给你一条平行于线段 AB 的直线 l 。请只用直尺作出线段 AB 的中点。
 
  
 

    你能想到该怎么做吗？

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

  

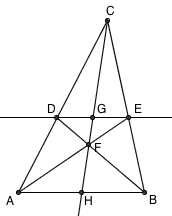
    在直线 l 的另一侧任取一点 C 。连接 AC 、 BC ，分别与 l 交于点 D 、点 E 。连接 AE 、 BD ，两线段交于点 F 。则 CF 的延长线与 AB 的交点 H 就是 AB 的中点。
    由于 △CDG 与 △CAH 、 △CEG 与 △CBH 是两对相似三角形，因此我们有

      AH:DG = AC:DC = BC:EC = BH:EG

    另外，由于 △AFH 和 △EFG 、 △BFH 与 △DFG 又是两对相似三角形，因此我们还有

      AH:EG = FH:FG = BH:DG

    注意到 AH:DG = BH:EG 以及 AH:EG = BH:DG 同时成立，等式两边对应相乘便可得到 AH = BH 。

 
    且慢，这只是一道热身题而已，有意思的现在才真正开始：

给你一条线段 AB ，请你用直尺和圆规作出线段 AB 的中点，不过在作图过程中你只能用一次圆规。

    这次你还能想出办法吗？

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

   

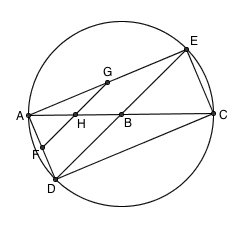
    以 B 为圆心， AB 为半径作圆。延长 AB 与圆交于 C ， AC 就成了圆的一条直径。过圆心 B 随便作另一条直径 DE ，于是四边形 ADCE 就是一个矩形。由于 AD∥EC ，因此借助前面讲过的方法我们能仅用直尺作出 AD 的中点 F ；类似地由于 AE∥DC ，因此我们也能找出 AE 的中点 G ；显然， FG 的连线与 AB 的交点 H 就是 AB 的中点。

 
    好了，如果前两个问题你都想到了的话，请准备好接受终极挑战吧：

给你一条线段 AB ，请你只用圆规作出线段 AB 的中点。

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

   

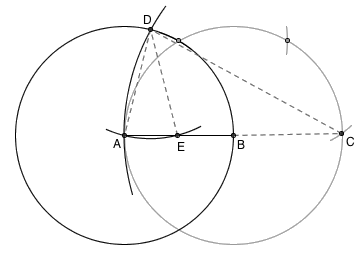
    以 B 为圆心， AB 为半径作圆。以 AB 为长度，从 A 点出发，在圆周上连续截取三次，得到点 C 。这个点 C 显然满足 AC ＝ 2AB ，它相当于是倍长 AB 后得到的点。现在，以 A 为圆心， AB 为半径作圆，再以 C 为圆心， AC 为半径作圆，两圆交于点 D 。以 D 为圆心， AD 为半径作圆，与 AB 交于点 E 。 E 就是 AB 的中点。
    这是因为， △CAD 与 △DAE 是一对相似三角形（它们都是以 ∠A 为底角的等腰三角形），而 AD 是 AC 的一半，因此 AE 就是 AD 的一半。而 AD 是等于 AB 的，因此 AE 也就是 AB 的一半了。
 

44 条评论

发表评论




Enter Captcha Here :