从cut-the-knot上看到的。
问题：
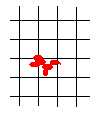
设想一个平面上布满间距为1的横纵直线，形成由一个个1×1正方形组成的网格。任意给一个面积小于1个单位的图形，证明这个图形总能放在网格中而不包含任何一个格点。
证明：
我们可以这样考虑这个问题：把图形随意放在网格中，如何移动网格使每个格点都在图形外面。
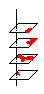
现在我们把给定的图形随意放在网格中。然后沿着网格线把包含有图形的网格切成1×1的小格子，从网格中拿出来。把它们重叠起来（不旋转），再想像这些格子是透明的，而图形是不透明的。从上往下看这一叠格子，你看到的会是这个图形的各部分重叠地放在一个格子中，仿佛一个沾有污渍的方块。很显然这些污渍不会布满整个方块（图形面积小于一个格子的面积），方块上总有一块干净的地方。现在我们用一颗针从一个干净的地方刺下去，把这些重起来的格子刺穿。把这些格子放回原来的网格中，你看到的会是每一个有图形的方格内都有一个针眼，这些针眼都不在图形内。现在可以把原来的网格擦掉了，这几个针眼可以看作是新网格的格点。按针眼的位置重画新的网格，那么这个图形内决不会有新网格的格点，此时，结论也就证到了。
做人要厚道，转帖请注明出处。
和闵可夫斯基定理有相似
回复：AsukaNoKaze果然是MO牛人
没有能够证明所剪下来的图形那样做不会重叠，所以证明无效！
回复：你没看明白吧。图形可以重叠，但因为总面积小于一个小正方形，所以总有空的地方
诡异
marvelous！[wink]
这样的证明。…想了好久才想通为什么有一条贯穿4个方格的线使这4个点都没有污滓..
好巧妙的证明..[cry]
诡异。。。
高!
说不出的高
“此时，结论也就证到了。”
这句话很有川味
回复：把“此时”换成“这个时候”更有川味
哥们儿，你咋是个文科？
3周年考古～
这个结论对分形图形（例如几乎布满整个屏幕的）也成立么？
成立！可以想象把所有无穷个的网格都叠起来。因为污渍面积小于1，所有必定有空白的地方穿针，就相当于把原来无穷多个方格都穿个洞。这个洞就是新的网格
奇妙。
神奇——+
天呐，我竟然错过了这么经典的证明，真的奇妙~
奇妙！！！
这个世界很奇妙。。
为什么
按针眼的位置重画新的网格，那么这个图形内决不会有新网格的格点
分形似乎需要补充
这种情况好像不行吧!
找四个相邻的方格,分别顺时针在四个方格的右下，坐下，右上，左上放四个面积0.25的小方格,这样针怎么穿都没有干净的地方啊
这种情况好像不行吧!
如果找四个相邻的方格,分别顺时针在四个方格的右下，坐下，右上，左上放四个面积0.25的小方格,这样针怎么穿都没有干净的地方啊
“22楼 这种情况好像不行吧!
如果找四个相邻的方格,分别顺时针在四个方格的右下，坐下，右上，左上放四个面积0.25的小方格,这样针怎么穿都没有干净的地方啊”
图形面积要小于1
谢谢23楼的提醒，是小于1啊,没仔细看题啊.
这个玩意让我想起了 只有正四边形 可以每个顶点都在格点上的证明
Amazing….
看了 你的博客..
我就不想 看书了..
真的…
你也该把原帖的地址写出来吧，我想看英文
好神奇啊!斑竹的证明实在是太妙了！！！
题目改成”对于任意给定的面积小于1的图形,都可以放置在由连续的1×1正方形组成的网格间,且满足以下条件,网格的格点不会落在给定图形上”.
然后,再使用你的证明,会更自然些.
我该说神马好呢……
果断留名
http://zhidao.baidu.com/question/228181033.html
http://zhidao.baidu.com/question/228181033.html
请看看这个怎么做
证明方法太牛了！佩服的五体投地！
能在细致一点吗，比如说为什么一定存在一个点，使得把四个方格重叠后，从这个点刺下去可以不碰到图形中红色的区域
wms357说的那个就是令面积小于1的圆与整个平面建立一一对应。但是其实按面积度量其已经改变，虽然一一对应，但相互对应的两点的测量之比不等于1，面积已经改变。
回楼上：
一个面积小于1的图形，在它盖到的每一个方格内，其所占据的点集加在一起不可能拼成一个面积为1的方格。
假设占据了n个方格，在第1个方格这个图形没有覆盖到一个区域G，在第2个方格里，与G相对于方格1的位置相同的是一块与G一模一样的区域，在这个区域里该图形又没有覆盖到一块区域H，在第3个方格里存在相对于此方格与方格2里的H一模一样的区域J。。。总有没覆盖到的区域X，因为图形面积小于1。
很巧妙。“4个针眼怎么连成单位正方形的格子”竟然让我想了一会。这也许就是空间变换的妙处之一，人如果能进入4维空间，也许很多问题就容易多了。
思考的乐趣祭奠点1
找四个相邻的方格,分别顺时针在四个方格的右下，坐下，右上，左上放四个面积0.25的小方格
搞笑，给你一个 3*三百分之99 的长方形，不就不行了？
针眼的意思，就是重新制定网格，有可能是斜着，但是当一个1*1的网格旋转到一个正菱形时，这也就是灵活的最大限制了。只要图形的长度或宽度，只要有一个一旦超过根号2，即其对角线，那就装不下了。 4*四百分之99,
5*五百分之99，装吧！
搞笑，给你一个 3*三百分之99 的长方形，不就不行了？
针眼的意思，就是重新制定网格，有可能是斜着，但是当一个1*1的网格旋转到一个正菱形时，这也就是灵活的最大限制了。只要图形的长度或宽度，只要有一个一旦超过根号2，即其对角线，那就装不下了。 4*四百分之99,
5*五百分之99，装吧！
不想吐槽40L了。。。
格线格点都分不清
40L你把问题看清楚了么？你牛什么牛？装不装得下是博主要证明的问题？2货
污点网格块数不只4个的时候,那些针眼也就不只4个了(理论上可以压缩成一条直线,经过格点对角线,长度即为无穷大),那么,怎么重绘 格点呢?
比较郁闷,是我哪里没想清吗?
望回复；
回复40Ｌ,直接把你那个长方形摆正来(垂直),不就可以了；
@43Ｌ我懂了… 膜拜大神!
请问怎么按照新的针眼重画新的网格
这个图形不一定只横跨四张正方形，如果有好几十张，如何重画新网格
这个证明巧妙是无疑的，但貌似博主在思考的乐趣一书中把这题吹得太过了
我给一个证明，也许没那么神奇，但能让大家明白这题是怎么编出来的
理解了这个证明，大家也许就会觉得本帖的证明就是给一个普通证明穿马甲。
取一个充分大的正方形，顶点都是格点，且包含此图案
然后修改图案所在的空间为这个正方形，并把这个正方形设为“循环”的
这样，对这个正方形而言，由于最上面一行的点就与最下面一行重合，它的面积就是它的内部格点数，设为n。格点设为A[1],……,A[n]
在正方形内部随意取一个点P。取n种颜色。
对所有正方形里的向量，试验原图案平移这些向量后得到的。如果它的内部有格点A[i]，就把P平移这个向量的反方向后得到的位置涂上第i种颜色。
这样，事实上，第i种颜色的区域就是原图案平移（A[i]->P）后得到的，面积小于1.
以下无需多说
我只能说，这个证明酷到毙了！！！
漂亮
一个有名的经论是说, 如果平面上一块面积大于n(非负整数)的紧区域, 则一定可以通过平移(注意不旋转), 使得这个区域能够盖住n+1个格点.
这个证明却不是严谨的,所以我对结论持保留态度。平面上的方块是比这些方块的格点少的，比如一个方块有4个格点，2个方块至少有6个格点，4个方块至少9个格点。用这里的证明里的图，4个方块用针刺穿，只有4个洞，以这4个洞为格点重新画图，只能保证这4个新格点不图形上，并不能保证其余的（至少5个）格点不在图形上。事实上很容易可以构造出和证明相反的例子！
Origin:
https://www.cut-the-knot.org/proofs/lattice.shtml
这个证明只考虑了平移但没考虑旋转。考虑旋转的话，我觉得面积小于π/2个单位的图形也能做到。我还没办法证明或举出反例，指望这里高人指点了： https://math.stackexchange.com/questions/4221406