史上最牛的Crossword | Matrix67: The Aha Moments

这是一个由 Lee Sallows 创造的谜题。下面这个 Crossword 中有 6 个横向短语和 6 个纵向短语。每个短语都是形如“多少多少个某某字母”的形式，比方说 “THIRTEEN NS” 、 “EIGHT ES” 等等，它表示整个 Crossword 中恰好就有 13 个字母 N ， 8 个字母 E 。由于整个 Crossword 中有 12 个短语，这就意味着 Crossword 的解里只含 12 个不同的字母。牛 B 就牛 B 在，这个 Crossword 有唯一解。你能找到这个解吗？

突破口就在中间一列只有 5 个字母的纵向短语，它只可能是 “ONE ?” 。而最底下那个含有 6 个字母的横向短语则只可能是 “TWO ?S” 、 “SIX ?S” 和 “TEN ?S” 。但填 “TWO” 和 “TEN” 都是不可能的，否则字母 O 和 N 就不止一个了。因此，这6个字母只可能是 “SIX ?S” 。那个最长的纵列只能是 “THIRTEEN SS” 、 “FOURTEEN SS” 、 “EIGHTEEN SS” ，但 “FOURTEEN” 是不可能的，因为不存在以 F 打头长度为 5 的数词。 “EIGHTEEN SS” 也是不可能的，因为即使算上可能出现的 “SEVEN” ， 12 个短语也还不足以产生 18 个 S 。因此，这个最长的纵列只能是 “THIRTEEN SS” 。以 T 打头长度为 5 的数词只有 “THREE” ，而以 “R” 结尾长度为 4 的数词只有 “FOUR” 。现在，我们已经确定了 12 个 S 的位置，还差一个 S ，而填 “SIX” 、 “SIXTEEN” 、 “SEVENTEEN” 的地方都没了，因此两个阴影单词中必有一个是 “SEVEN” 。

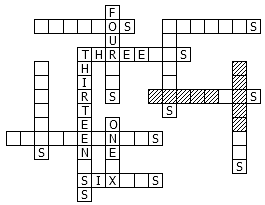
中间那个还没填的纵列只能是 “FOUR ?S” 、 “FIVE ?S” 、 “NINE ?S” ，但 “NINE” 是不可能的，否则就不止 3 个字母 “N” 了。因此 “SEVEN” 不在横向的阴影位置，否则 E 的个数将不止 4 个或 5 个。那么 “SEVEN” 只能在纵向阴影位置。此时，我们已经确定了 Crossword 中的 12 个字母分别是 EFHINORSTUVX ，没有字母 G ，因此横向阴影不会是 “EIGHT” ，只能是 “THREE” 。对比已有字母的个数和未填的短语，剩下的空格很快就能完成。以下就是这个 Crossword 的唯一解：

22 条评论