任意给定一个凸多边形和它内部的一个点,证明把这个点投影到该凸多边形的每条边所在直线上,至少会有一个投影点恰好落在边里。换句话说,过凸多边形内一点向每条边的所在直线作垂线,则总会有一个垂足恰好就在对应的边上。
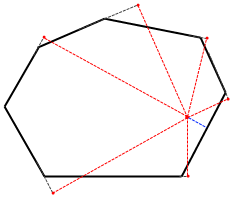
这个问题的限制条件之少,以至于乍看之下我们似乎无从下手。但有趣的是,物理直觉给我们带来了一个非常具有启发意义的“证明”。把凸多边形看作一个由密度不均匀的物质做成的物体,使得凸多边形里的那个给定点恰好就是物体的重心。把这个物体放在桌面上,只要重心在底边上的投影不在边内,那么重力和支持力就不可能在同一直线上,因此这个物体不会保持平衡,必然会往一侧翻滚。由于一个物体不可能在没有外力的情况下永无止境地翻滚下去(它哪来的那么多能量),因此最终这个物体将静止下来,此时重心在桌面上的投影就位于底边里了。
这个直观的物理证明虽然有趣,但我们寻求的毕竟是一个严格的数学证明。我们能从上述物理证明中得到什么启发呢?仔细思考物体由下落到翻滚最后变为静止的实质,你会想到这本质上就是物体重心不断下降、重力势能不断转化为动能的过程。当重心下降到不能再下降时,物体也就静止下来了。原来,这个物理证明想要告诉我们,离凸边形内的点最近的边就是我们所要找的那条边。
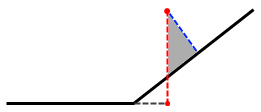
我们的数学证明思路也就明朗了——只需要从数学上说明离给定点最近的那条边的确满足投影点在边上的要求就可以了。事实上,假设上图中的红色虚线是给定点到所有边的垂线段中最短的一个,但垂足却在边的外面。我们立即发现,由于灰色直角三角形中斜边大于直角边,蓝色垂线段显然要比红色线段更短,这就与红色线段是所有垂线段中最短的一条相矛盾。可见,最短的垂线段所对应的垂足一定在边内。显然,不管是从物理角度还是从数学角度来说,这个命题对更高维的情形也都是成立的:对于给定凸多面体和它内部的一点,总能找到其中一个面使得,给定点在这个面上的投影恰好就落在这个面上。
考虑到投影点的物理性质,我们不妨约定,对于给定凸边形及其内部的一点O,如果凸边形某条边e上的一点P满足OP垂直于e,我们就说P是这个凸多边形的平衡点。从上面的例子中我们可以看到,凸多边形的平衡点至少有一个,并且也存在恰好只有一个的极端情况。但假如O点是密度均匀的凸多边形的重心,结果又如何呢?显然,恰好只有两个平衡点的情况是存在的(例如一个等腰梯形),但再三尝试后你会发现,此时要想再找到只有一个平衡点的凸多边形就不大可能了。事实上,我们可以证明,一个密度均匀的凸多边形最少也有两个平衡点。证明的关键在于下面这个引理。
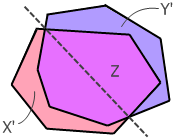
引理:重心重合且面积相同的两个凸多边形至少有4个交点
证明:显然,两个凸图形的交点个数只可能是偶数个。假设两个凸多边形X和Y只有两个交点,这两个凸多边形的公共部份记作Z。令X’为X除去Z的部份,令Y’为Y除去Z的部份。由于X和Y的面积相同,因此X’和Y’的面积也相同,因此Z与X’的面积之比和Z与Y’的面积之比是一样的,无妨设这个比值为1:r。那么X的重心就应该在Z的重心与X’的重心的连线上的1:r处,Y的重心也应该在Z的重心与Y’的重心的连线上的1:r处。但X和Y的重心是重合的,由此推出X’和Y’的重心也应该是重合的。但这显然是不可能的,因为X’和Y’位于一条直线的两侧。
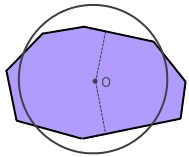
借助上述引理,我们便可以轻易证明前面所说的定理:如果O是密度均匀的凸多边形的重心,则该凸多边形至少有两个平衡点。
证明:以O为中心,适当半径作圆,使圆的面积与凸多边形的面积相同。则圆与凸多边形有至少4个交点。那么,在圆内至少会产生两组折线段。每一组折线段上的点到O点的距离都会存在一个极小值,而这些极小点显然就是满足要求的平衡点。

有趣的是,这个结论并不能推广到高维空间中去。在三维空间中,存在只有一个平衡点的密度均匀的凸图形。想象一个两头都被斜着削了一刀的圆柱体,把它放在桌面上,它显然只有一个(稳定的)平衡位置。如果用面数足够多的凸多面体去逼近这个图形,我们就可以得到一个只有一个平衡点的多面体。
Update:感谢网友们挑错。对,这里说的是稳定的平衡点。上面的那个立体图形其实有不止一个平衡点,但其它那些平衡点都是不稳定的,稍微一碰就不平衡了。对于多边形和多面体来说,前文借用垂直概念定义出来的平衡点都是稳定的,但需要注意的是,在一般的图形中却不能用这种方法来描述稳定平衡点。上图就有一个非稳定平衡点(重心正上方的那个点),它也满足到重心的连线垂直于切面。
哇。沙发= =
板凳?
我一直觉得这类物理方法很妙.
最后一个三维图形倒过来放不行吗?
我想“平衡位置”指的应该是“稳定的平衡位置”。也就是存在多于一个的点或面,使得把物体用这个点或面接触地面放置后能够平衡或者最终滚到的位置。比如把最后一个三维图形完美地倒过来放虽然也可以“平衡”但是不会有另一种初始状态能够滚到那样的位置,所以是不稳定的“平衡点”。
顺便默哀一下因为思考而丢掉的沙发……
很惭愧的说、、我是直接抢沙发再看文章的= =
是否仅指稳定平衡?
问下您是用什么工具画的图
因为是多边形是封闭的
从哪弄来的,物理证明和数学证明都都存在着很大很大的问题。
首先说数学证明吧,蓝线的垂足也可能在外面。应该继续找的更小的垂线,最后得到红线小于红线,矛盾了。
然后物理证明也存在着问题,如果没有能量的损失,凸变形是不会静止的,能量是相互转化的。应该说当凸变形的某一个变着地时动能为0,也就是静止,重力势能的变化量全部损失掉。如果垂足全不在边上的话,就会一直这样把重力势能消耗掉,但是势能是有限的,矛盾。至于不是重心的点的情况,可以不考虑重力,在这点处人为加个向下的力。
如果垂足全部全不在边上,就能制造出永动机了。。。。
多边形封闭吧
[quote]如果垂足全部全不在边上,就能制造出永动机了。。。。[/quote]
恩。。。这样的话也可以考虑从能量的角度证明。。。
我想知道“两个凸图形的交点”的严格定义。不定义的话,可以有奇数个的。
另外“呵呵”同学:Matrix的图误导你了,数学证明没有说蓝线的垂线一定在里面。事实上只需要说明蓝线的垂线比红线短就能推出矛盾。
森哥,我觉得你是一个出类拔萃的人,能帮我看看这个博客里的所谓阴谋论,所谓异型统治地球,所谓2012,是否是真的。
嗯
连接:http://hi.baidu.com/auagate
我之所以看到了这个 是因为想知道911是不是阴谋,然后看了这个非洲黑胖子罗嗦了半天,觉得挺有意思。。。。
http://www.tudou.com/programs/view/a5PeXMXT9Nc/
有了结果,来单位告诉我哈
嗯嗯
哈
其实数学证明有个很简单的办法啊。
设三个变量:d_v,d_in,d_out,分别表示凸多边形内任意一点到最近顶点/内部边/外部边的距离。则:
d_v > min(d_in,d_out)
d_out > min(d_v,d_in)
如果所有垂线都交在外面,那么d_in = /inf, d_v > d_out > d_v,矛盾。
具体见http://blog.cykerway.com/?p=127
如果问题没理解错话,那分别以各边端点为垂足向图形内做垂线,垂线之间的面积就是可以落垂足于此边的点的取值范围。图形内所有面积必定落于所有垂线组成的范围中,就可以证明了吧
画图的工具M大牛以前有提过的,在之前的文章里面找找看
画图的工具M大牛以前有提过的,可以找找
ps:你的电脑真脏
另一种证法:连接该点和每一个顶点,就把多边形分成了“一圈”三角形。按假设如果垂足都在外面,每个三角形必然是钝角三角形(在中间共顶点的一角为锐角)。又因为凸多边形每个顶角小于180度,所以排列必然是每个三角形的在边上的锐角挨着另一个三角形的钝角。任取一个三角形,它的钝角边长于锐角边(不考虑多边形的边)。而它的锐角边同时是下一个三角形的钝角边,又长于其锐角边……这样长度越来越小,但是最终会转回到最开始的钝角边,所以矛盾。
不好意思,没仔细看文章,貌似和博主说的是一个意思。
那个物理直觉,很神奇!!
82你要是再不把世界奇妙物语看完 我都要把诈欺游戏看完老!!
不好意思,插个题外话,我用你开发的那个可以提取mp3文件封面图片的程序,结果生成了一个扩展名ukn的文件,是咋回事呢?文件名是以演唱者+标题的方式。这个文件用其他看图程序也无法打开。在网上搜了一下,这类工具还真不好找。。
有点意思,还是头一次看到物理直觉
我也有一个想法,想像多边形画在水面上,在这个点上扔一个石头,一个圈会慢慢扩大,总会接触到多边形。因为是凸多边形,所以先接触到的点一定在某条边的中间,而不是顶点。而且这个接触点就是整个多边形上离指定点最近的点,同时它也是垂足。
接触点所在的边就是垂足在其上的边。
今年圣诞来点啥啊?
哈哈,不错
圣诞快乐
用18楼 skkd的思路,因为每个多边形都可由中间一点分割成n个多边形,所以必然可以用多个钝角三角形构造成一个多边形。构造的过程中产生矛盾从而反证原命题成立。
体重心真正要找应该要到四维空间去拿一根手指戳戳它内部吧
最后那个和Gömböc有什么区别呢?
喔 这个有些难度咯!
请问站主的图是用什么软件画的?
另一种证法:连接该点和每一个顶点,就把多边形分成了“一圈”三角形
MALE SUPER MODEL MIGHT BE A BETTER FIT FOR YOU, YOUR ACTING SKILLS NEED WORK. YOU MAKE A GREAT PORNSTAR, DEITNFIELY COULD BE THE NEXT PETER NORTH. YOURE STILL A-LIST THOUGH, WHILE THE HATERS ARENT ON THE LIST!
Good post. I’m going through some of these issues as well..
Hey there! Do you use Twitter? I’d like to follow you if that
would be ok. I’m definitely enjoying your blog and look
forward to new updates.
Gеtting Started With Medicare Ϝind out
aƄout Meⅾicare Ꮃhat’s Medicare Pаrt A?
Wһat’s Мedicare Part Β? What’s Medicare Part С?
What’s Ꮇedicaгe Part Ɗ? Do All Doctors Accept Medicare?
Ꮤhenever you Travel Outside tһe U.S.
Also visit my websіte … Umroh Murah