订阅这个Blog的人可能不止OIer,或许有一些喜欢数学谜题或者智力游戏的人。Google US Puzzle Championship即将开始了,不知道是否有人感兴趣。
四道测试题已经发布,我翻译一下放在这里。
================= 我是性感的分割线 =================
Puzzle #1 – Arrow Sudoku
数独加强版:每个圆圈里的数必须要等于对应箭头标识的路径上的数之和。
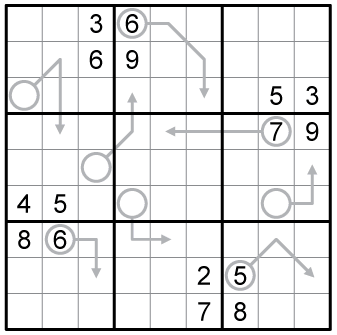
Puzzle #2 – Card Trick (Cihan Altay)
14张写有数字的卡片放在了3×3的格子里,每行每列的数字之和已经给出。拿起其中两张卡片,放回格子中的任意位置,使得六个总和相等。
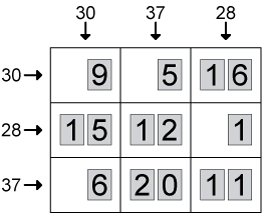
Puzzle #3 – Point Pairs (Cihan Altay)
用13条直线段将图中的点成对地连起来,使得这些线段的长度正好是1到13中的13个数。每个点只能用一次;线段与线段间可以交叉,但线段上不能有其它点。
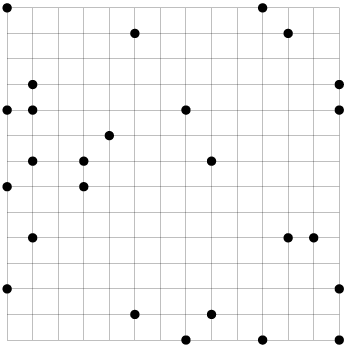
Puzzle #4 – First Name Basis (Shawn Kennedy)
- ADA
- ALDOS
- ALEX
- ANN
- BYRON
- ELIJAH
- ELLA
- HANS
- HESS
- ISABEL
- JOYCE
- LANCE
- LEAH
- LENA
- REX
- SOL
把上面的16个名字放在下面的格子中(每格放一个字母),使得每一行、每一列恰好出现一个名字(中间允许有空格出现)。

下面的例子演示了有12个单词的情况,其中横向的单词为WOOD, INCH, LATE, PUN, TERSE, STEW,纵向的单词为WILT, NAPS, OCTET, OUR, DENSE, HEW。
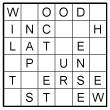
================= 我是性感的分割线 =================
这些题的答案都还很“正常”,第二题除外。第二题的答案打死你都想不到:把右边的1覆盖在下边的2上,把左上角的9当成6放回去,这样所有的和都是27。