说勾股定理是一切科学的基础恐怕一点也不夸张。一些最基本的物理定律就与勾股定理之间产生了完美的对应。在我初三学到动能的公式时，我就想到，动能与速度的平方成正比是有内在原因的，这正是由数理科学中最基本的定理——勾股定理——决定的。考虑一个质量为1的物体向正北方向运动，如果它的速度为a，那么所需要的能量就是(a^2)/2；类似地，让同一个物体以b的速度向正东方向运动，所需要的能量应该为(b^2)/2。如果把这两个力叠加在一起，我们就得到了这样一个事实：用(a^2)/2 + (b^2)/2的能量可以让物体往大致东北的方向运动，其速度正好就是一个以a和b为边的矩形的对角线长。因此，(a^2)/2 + (b^2)/2正好也就是对角线长度的平方的一半，这恰好与勾股定理的内容一致。可以说，我们用数学定理验证了一个物理定律；也可以说，我们用物理定律证明了一个数学定理。
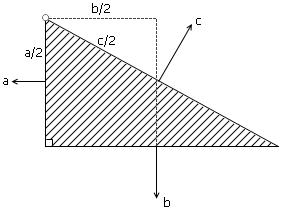
让我们来看另外一个更巧妙的例子：考虑一个底面为直角三角形的棱柱形盒子，其中一个锐角顶点（所对应的棱）固定在一根转轴上，因此整个盒子可以绕转轴转动。在盒子里面倒满水。在没有外力作用的情况下，这个盒子会绕着转轴自己转动吗？显然不会。这表明，盒子中的水对三个竖直表面的水压所产生的力矩是平衡的。每个面的压力大小都和直角三角形的对应边长成正比，它到转轴的距离也正好是每条边的长度的一半。两个直角边上的水压把棱柱往顺时针方向推，斜边上的水压则把棱柱往逆时针方向推。这样，前两个力矩应该与后一个力矩平衡，即(a^2)/2 + (b^2)/2 = (c^2)/2。（补充一下：a、b、c分别表示直角三角形的三边长）
本文来源：http://www.cut-the-knot.org/pythagoras/MechanicalProofs.shtml
这个。。。即使勾股定理不成立，盒子也不会转的吧。。。
水是在盒子里面呀
这个跟液体压强之类的有关吧，大学物理没学好，不乱说……
话说有个用量纲的证明也很有趣
有必要解释一下最后一句话abc具体指的是什么
后者足够牛X
大半夜的竟然又发一篇…
。。。。。。MM67您最近鸡冻了= =||。。。
@bigworm
abc==三个竖直表面的水压所产生的力矩
最近勤奋了啊，很好
这篇太水了，严重误导粉丝群众……
第一个问题谈不上验证，最多只能说是自证；
第二个问题孤立系统的外力和内力没搞清楚；
Matrix你还是讲数学吧，物理真不是你擅长。
昨晚安装MATLAB7.0失败了- –
http://kshaoye.com/images/xj4/mat.jpg
第一个问题……如果两个方向的夹角不是90度……比如53.72度……那按您这么说就出事儿了……
我想问下各位这种示意图都是用什么软件画的-_-~~
挺有趣的, 但是也同样觉得只能说是一种验证吧.
@wecing
为什么捏？？喵。。。
@A13
两个方向的动能和是A^2/2+B^2/2……那如果合速度大小为C……不就有C^2=A^2+B^2了吗……
不错..
@流水弦歌：第二个问题 研究对象选取的时候 只选取外壳 不把水选进去就可以了
其实楼主是本末倒置，本来很多物理定理都是依赖于代数及几何来推导的，所以说勾股定理的物理证明其实只能是一个必要条件而不是证明的充分条件。就好像在物理里合力1N + 1N = 2N, 并不能说明数学里的1 + 1 = 2。
支持1 2 10 12 14 18楼
本文纯粹是瞎扯淡
yh牛，说得有点过了……
sigh。。。
loooooool…
对不起，我说错了，仔细思考后发现，确实能证明（或者说验证），不过我发现勾股定理仅仅是本方法能够验证的一小部分，经过推广之后我得到：
平面内有一点O和任一曲线C，P是C上任一点，则有：OP向量点乘dl向量再乘以单位向量n的积对于曲线C的环路积分为零，其中单位向量n垂直于向量dl并指向曲线外。
感觉这是个非常简单的结论，但我无法再化简，如说错了请指教。
是的，其实是循环论证~~:D
这篇文章很不错的。和爱因斯坦同学”物理现象的本质是空间几何结构的反应”的看法比较一致。你看，因为低速情况下，空间近似平直，于是勾股近似定理成立，动能的速度平方定律近似成立。极端高速情况下，广义相对论下空间弯曲（勾股定理已然不再成立），这个时候动能不再正比于速度平方了
虽然还没有仔细推理过@M67的有关勾股的问题，但就算激动（有想法后的经常表现）而考虑不周，也不应得到所谓扯淡，无聊这样的回复，毕竟有想法就是好的，而不是发现别人的错误还显摆自己技高一筹更值得表扬！戾气退散 -_-# 好像是第一次发留言。
>>这个。。。即使勾股定理不成立，盒子也不会转的吧。。。
right
>>对不起，我说错了，仔细思考后发现，确实能证明
wrong
力矩的方向不是那个样子滴
那啥…这不就是矢量合成…
我秃然想到,如果勾股定理不是现在这个形式,那么相对论……
第一个不加验证地用了一些物理规律，比如E∝v²，以及能量之间可以简单地相加。
第二个显然是热力学没学好
假如勾股定理不成立——我们的物理空间不是欧氏的——三角形会转起来吗？
这都是互相决定的吧…无所谓哪个证明哪个…不然公理是干什么的…
看起来很有道理
只是有个小问题：在真实的物理空间中勾股定理并不严格的成立…
感觉第一个有些牵强，不是很理解
第二个还是很有道理的，事实上，对一般三角形来说，还可以推出余弦定理。看到有人所外力内力没搞清楚，事实上单独把盒子作为一个整体就OK了。。
好像第一个确实是有问题。因为能量是合速度的平方，而不是分速度的平方，作者那样求一开始其实就是用的了勾股定律。
这也就解释了12的那个疑惑。
至于第二个，确实挺巧妙，没什么问题。
10楼才是误导大家呢，博主这篇内力和外力搞得非常清楚。
盒子加水这个整体受到的外力是零；而盒子受到的外力就是水给它的压力。
但我仍要说，这是循环论证。
因为这里用到了液体压强各向相等这个定理，而这个定理不是凭空出现的，这个定理的得出就用到了勾股定理。
很抱歉，我仔细想了一下，发现我楼上说的也是误人子弟。
液体压强各向相等的推导，并不需要用到勾股定理。
博主这两个证法我目前看来并没有问题，而且我发现，这两种证法之间有深刻的内在联系。
（接楼上）
液体压强各向相等的推导，用到的是力的分量独立性。这里我就不具体说了，大家可以在任何一本流体力学的教科书里找到具体的推到方法。
而第一种动能证法也用了力的分量独立性。
（待续）
更重要的是，两种证法其实都隐含地用到了如下关系：
∫ax dx = (1/2)ax^2
液体对盒壁的压力矩是 ∫Fa da = (1/2)Fa^2
而从零开始加速的位移是 r = ∫at dt = (1/2)at^2
所以才会有动能：F*r = ma*(1/2)at^2 = (1/2)m(a^2)(t^2) = (1/2)mv^2
为什么矢量的分量独立性，加上 ∫ax dx = (1/2)ax^2 这个关系式，
就能得出勾股定理，背后能后想出来的数学实质是什么，我要去好好想想。
打错了，是“背后能抽象出来的数学实质是什么”
经过几天的思考，最终抽丝剥茧得到这两例的数学实质就是
r^2 = 向量r ^2 = x^2 + y^2
就是那么简单，木有什么新发现，哎。。。
41楼问：为什么矢量的分量独立性，加上 ∫ax dx = (1/2)ax^2 这个关系式，
就能得出勾股定理?
我想了一下，ax积分产生(1/2)ax^2这一过程，就相当于计算了一个两直角边分别长a和x的三角形的面积，里面已经悄悄用了勾股定理。
第二个水桶的例子里，你之所以能把每面壁上的力矩简化为出自中点的一个与边长成正比的力的力矩，其实也是已经悄悄用过了一个积分。就是沿整条边的微分力矩的积分，这个积分也一样相当于计算了一个直角三角形的面积，也就是已经悄悄用过勾股定理了。
44楼有点错，应该是 “相当于计算了一个两直角边分别长x和x的三角形的面积”。
以上想法中，第一例矢量的分量独立性和第二例中水桶不会转确保了最后的积分总和不变或为0，而分量分别积分成三角形面积的过程引入了变量的2次方。又想了一下，这个引入2次方的过程似不能算作隐含使用了勾股定理。还要好好想想。
刚发现，这帖很老了，希望还有关注。
46楼，积分是比勾股定理更一般（更强）的定理（代数中无法说定理吧）。它不仅可以计算直角三角形的面积，连曲边梯形都可以计算。
其实m67牛已经说的很清楚了，是验证。但既然是验证，就是证明。（难道物理学意义上不是这样吗？）
两个方向的动能和是A^2/2+B^2/2……那如果合速度大小为C……不就有C^2=A^2+B^2了吗……