《几何原本》的命题1是“作以给定线段为边的等边三角形”，其做法也正如大家所料：以AB为半径，分别以A、B为圆心作圆，交点C就是等边三角形的第三个顶点，于是连接AC和BC即可。《几何原本》的命题2则是一个看似更加简单的作图问题：给定点A和线段BC，作以A为其中一个端点的、长度等于BC的线段。我原以为《几何原本》的做法也和我们平常的做法一样——以A为端点向任意方向作一射线，再用圆规截取出和BC等长的线段。因此，每次在网上看到关于《几何原本》命题2时，我都会直接略过去。最近我才发现，《几何原本》中命题2的做法和大家想象的完全不一样，因为这种做法在《几何原本》中是不允许的。圆规只能用来作圆，不能用来度量和转移长度；换句话说，公设3中的“圆规”是一个“松”的圆规，一旦离开纸面后圆规的两脚便会“啪”的一声自动合拢。在这种条件下，你又如何实现上面提到的作图问题呢？
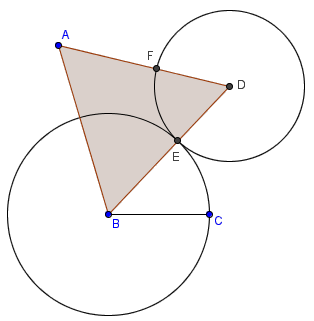
《几何原本》中的方法非常巧妙：首先，利用命题1作出等边三角形ABD。然后，以B为圆心，BC为半径作圆，交BD于E；然后，以D为圆心，DE为半径作圆，交AD于F。由等边三角形的定义，AD=BD；又由圆的定义，DF=DE；再由于等量减等量，于是AF就等于BE。再次利用圆的定义可知，BC也是等于BE的；最后由于“等于同量的两个量相等”，因此AF=BC，命题成立。
呵呵 撒花 偶像啊
一般M牛长时间不更新，过一段时间就会有牛文
画圆不也是在转移长度吗?
@楼上
但是你圆规的两脚不用腾空啊
这次隔的时间好长
GeoGebra画的？
给定一个方向的话，如果用这个方法，未必太烦？
ps如果咫尺是歪的，怎么办？或者说，有个不规则的平面的物体，能用来作图吗？
。。。。
牛
M67难得火星了啊……
圆规是松的，以至于一端离开纸面就会合拢。
大家有没有做过试验？
即使圆规不离开纸面也画不出指定半径的圆的，不信做试验去
在这种情况下根本画不出规则的圆，或者根本画不出圆来(起点和终点很可能不能重合在一起)，那几何原本中的那个方法第一步就成立不了
在下愚见
这个应该有很多别的方法吧，比如说直D为A点，直接做AB垂直平分线，再做出E关于这条线的对称点K 此时BE=AK
是不是可以认为是在圆轨上绑了一条橡皮筋？
松规？画螺线比较方便。
非常经典！！！
顶一个，买一本《几何原本》研究一下
请问以下问题楼主有什么高见：
define the set A={(x,y)belong to R^2,X^2+y^2 小于等于1}， and the point b=(3,3)belong to R^2. find all hyperplanes separating the set A and the point b.
Hint:
a)provide a graphic sketch of the problem
b)break the problem into three or more simpler subproblems
c)slove these subproblems one by one,starting with the simplest
我正在看《几何原本》，看到命题2后，有点迷糊，想到了这篇文章，原来圆规是不能用来转换长度的。
非常经典！！！
当BC既大于AB又大于AC时，上诉办法不能直接使用，但原理是类似的要，以BC为边做全等三角形。
在用单规确定圆弧和线段的交点时，圆规可以用来转移长度吗？《思考的乐趣》单规作图的力量P125
我没想通“以BC为边做全等三角形”的做法。我想的是，以C为圆心BC为半径画圆，圆上总能找到一点B’，满足AB’大于B’C。用B’代替B执行原操作。
那松规作图是否和单规作图等价?