一个实际问题：如何放本本使得其占地面积最小？

    我的书桌已经乱到一定的程度了，以至于每次把笔记本从包包里拿出来，准备把它放到桌子上去时，我都要在桌子上非常下功夫地寻找一块能够放得下本本的空地。久而久之，我开始思考：怎样放置笔记本才能使得它占据桌面的面积最小，而又保证它不会掉下去呢？

 

    直觉告诉我们，最优的放置法应该是让笔记本中心正好与桌角重合，且与桌面的直角边成45度角（如图1）。假设笔记本的宽度为1，则该方案占据了1/4个单位的面积。我们猜测这个解不可能更优了，毕竟这是最对称的一个解。证明这个结论很简单。我们先来考虑笔记本重心与桌角重合的情况。

 
 

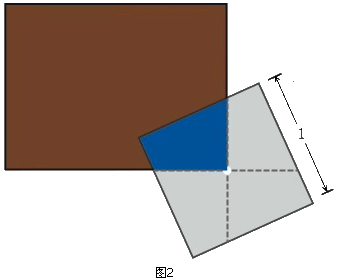
    假如我们的本本是正方形的话，问题就直接解了：不管以什么角度放在桌子一角，只要重心与桌角重合，所占的面积必然是1/4个单位（图2）。

 
 

    对于长方形的本本，只需要考虑长方形内所含的正方形（如图3）。可以看到，1/4个单位的面积（蓝色区域）无论如何都不会消失；想要消除图3中多出来的那块红色区域，我们必需把本本像图4那样成45度角地放置。

 
 

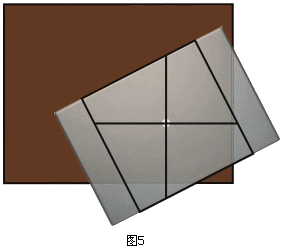
    至于重心不在桌角的情况，道理和上面一样：用沿桌子直角边平行的线把本本区域里的那个正方形分成四等份，则左上角那块区域一定在桌子内，因此，无论如何本本占地面积都不会小于1/4。

 
 

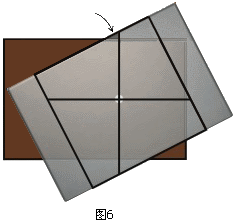
    注意到，上面的这些证明都假设我的桌面足够大，或者说桌子有两条边靠墙。如果本本下面用的是床上小桌板呢？此时，如图6所示，上述的证明不再成立，因为桌面太小可能导致那1/4个正方形伸出桌面。下面我们说明，假设桌子的宽度至少也是1个单位，那么1/4这个解依然是最优的。

 
 

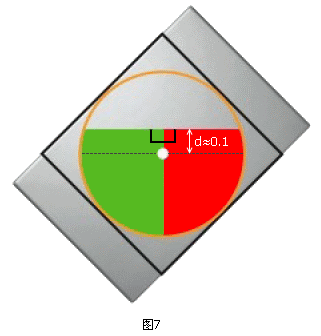
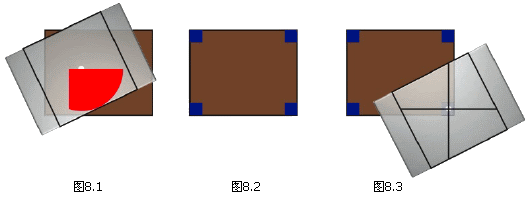
    如果桌子宽度至少有1个单位，那么不管本本的重心在哪里，它到桌子四条边的距离中至少有两个超过了1/2。因此，桌面内必然能容得下一个半径为1/2的90度扇形。不过，这个扇形的面积只有大约0.2的面积，离我们的目标还有一定的距离。为此，让我们考虑在正方形的内接圆中作一块面积恰为1/4的图形，如图7。红色和绿色区域的面积均恰为1/4，据计算可知超出中心的那部分宽度大约为0.1。这样，不管本本怎么放，桌面上几乎总能容下一块红色区域或其旋转、翻转后的图形，除非本本的重心和离它最近的两条边的距离都小于0.1（图8.2中的蓝色区域）。而在这种特殊情况下，之前的那种老的证明方法又管用了，因为1/4个正方形的“高度”或者“宽度”不会超过根号2的一半，约为0.7，它不可能超出桌面的另一端。

本文来源于这篇论文。原文中还有一些有趣的结论，感兴趣的话可以看看。

47 条评论

发表评论




Enter Captcha Here :